Deep Learning Basic - to Know

緣起

去年在寫 LLM 三部曲時，曾經提過要來寫一篇深度學習基礎文，目的是深入簡出的闡述 AI 背後的設計原理。如今生成式人工智慧已經深入各行各業，舉凡寫程式、寫文章、設計發想、客服語音等，到處都有 AI 的身影，也是時候履行之前的諾言了。

回顧人工智慧的過往，可謂是一段高潮迭起的歷史。早在古希臘時代，無數哲學家、數學家就試圖以基本的邏輯原理來解釋人類思維的運作。作為理性主義的代表，亞里斯多德提出「三段論」，即大前提、小前提、結論（如：人都會死、我是人、我也會死），認為思維可以透過嚴格的規則來描述和推導。 1936 年，Alan Turing 提出了「圖靈機」的概念 ¹，透過將思考模式編碼成一系列的規則，以符號讀寫的方式來模擬其運算過程。這種方式又稱做符號主義 (Symbolicism) 或邏輯主義，主張用公式來搭建智慧系統，是現代計算機的基石。

與符號主義相對的學派是聯結主義 (Connectionism)，主張知識是從感官經驗中累積而成，希望透過工程的角度重現神經元的連結，以此來模擬大腦的思考過程。 1943 年，Warren McCulloch 和 Walter Pitts 提出了神經元模型 ²； 1958 年，Frank Rosenblatt 提出了感知器 (perceptron) 模型，也是現代神經網路的起源。這兩個學派持續爭論與消長，帶來大量的研究和討論，可謂 AI 早期的黃金時期。

兩大學派反應了思考的演繹 (hypothetical-deductive, 左圖) 和歸納 (inductive, 右圖) 機制。 ³

1950 年，Alan Turing 提出了「圖靈測試」⁴，認為機器若能在對話中模擬人類的反應，即具有智慧。 1956 年， John McCarthy 等人舉辦了一場在 Dartmouth College 的會議，首次提出「人工智慧」(Artificial Intelligence, AI) 這個名詞，揭示其作為一門學科的肇始。在會議中，Allen Newell 與 Herbert Simon 提出了 Logic Theorist 程式，成功推導並證明《數學原理》中的大量定理。他們於隔年提出 General Problem Solver 程式，透過分治法 (divide and conquer) 來解決各種問題，廣受推崇。

在這個時期，符號主義是顯學，人們專注於在各個領域中建立知識的搜尋演算法。 Marvin Minsky 更曾言：「Within a generation... the problem of creating "artificial intelligence" will substantially be solved.」 1969 年，他出版了《Perceptrons》一書，指出單層感知器無法解決 XOR 問題，讓聯結主義備受冷落。當時的資金大量流入符號主義實驗室，前景看似繁榮，卻始終無法取得更進一步的突破。儘管演算法可以解決邏輯問題（如下棋），但卻無法有效處理感知問題（如辨識物體）。定義規則的過程需要對常識有著足夠的認知廣度，而過度的設計會造成組合爆炸 (combinatorial explosion)，使得許多問題需要花費指數時間來解決。這對當時的計算機硬體無疑是沈重的負荷。於是在 1970 年代，熱度衰減、資金撤出，人工智慧迎來了第一個冬季。

1980 年代，人工智慧的重點轉向建立特定領域的專家系統 (Expert System)。比較著名的有化學專家 DENDRAL、醫學專家 MYCIN 等，許多公司開始建立團隊，著手開發自己的專家系統。當時主要使用的程式語言是 Lisp，所以這類專門設計給人工智慧做搜尋優化的機器又被稱作 Lisp machine。然而榮景不到十年，以 Apple 和 IBM 為首，更加便宜且通用的個人電腦開始普及。昂貴的 Lisp machine 逐漸乏人問津，專家系統的熱潮也開始消退，人工智慧迎來第二個冬季。

在符號主義當道的時代，聯結主義的研究者仍在默默耕耘。 1986 年，David Rumelhart 和 Geoffrey Hinton (後被稱作 AI 教父) 等人提出了反向傳播演算法 (backpropagation) ⁵，使得多層感知器 (MLP) 可以被訓練，基本解決了 XOR 問題。 1989 年，AT&T 貝爾實驗室的楊立昆 (Yann LeCun, 現為 Meta 首席科學家) 將反向傳播應用在卷積神經網路 (convolutional neural network, CNN) 上，成功辨識出手寫數字 ⁶。 1998 年，楊立昆團隊進一步推出 LeNet-5，結合兩個卷積層和三個全連接層，是現代 CNN 的始祖 ⁷。

Architecture of LeNet-5. ⁷

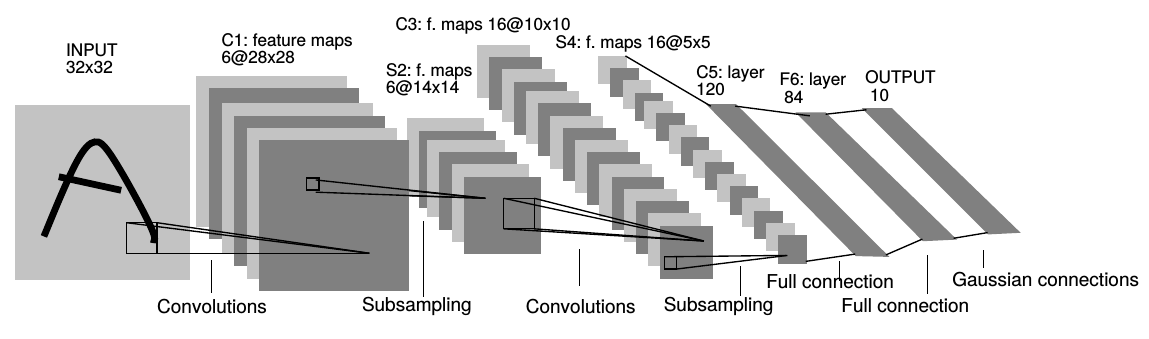
然而 CNN 有個問題，那就是計算太過複雜，當時的 CPU 難以負荷，導致其發展受限。 1990 年代，支援向量機 (support vector machine, SVM) 和隨機森林 (random forest) 等結合傳統統計學的演算法興起，能夠在小資料集表現得更好。在這時期，機器學習 (machine learning) 逐漸取代基於專家系統的人工智慧成為主流說法。

2009 年，李飛飛等人推出 ImageNet ⁸，這是一個經過大量分類標注的圖像資料集。 2012 年，Geoffrey Hinton 與其學生 Alex Krizhevsky 開發的 AlexNet ⁹ 贏得該年 ImageNet 大規模視覺辨識競賽 (ILSVRC) 冠軍，錯誤率明顯低於第二名。 AlexNet 使用許多近代方法，例如使用 ReLU 激活函數、引入 dropout 層、使用 Nvidia GPU 加速訓練等，揭露 CNN 的研究進入新的紀元。 2014 年由 Google 推出的 GoogLeNet (Inception V1) 獲得冠軍，深度達 22 層 ¹⁰；2015 年由 Microsoft 推出的 ResNet 獲得冠軍，深度達 152 層 ¹¹。有了 GPU 的輔助，學者開始探索更深的神經網路，開啟了深度學習 (deep learning) 的新時代。

也是 2015 年，Sam Altman 與 Elon Musk 等人成立 OpenAI，開始探索通用人工智慧 (artificial general intelligence, AGI) 的可能性。 2016 年，Google DeepMind 團隊結合符號主義的蒙地卡羅樹搜尋與聯結主義的神經網路，推出圍棋程式 AlphaGo，擊敗了九段職業棋手李世乭，引發全球對 AI 的關注。 2017 年，DeepMind 團隊進一步發表經典論文「Attention Is All You Need」¹²，推出了 Transformer 基礎模型，讓自然語言處理 (natural language processing, NLP) 也能透過 GPU 進行全面加速。至此，神經網路的複雜度開始暴漲，從百萬級參數逐步進化到千億級參數。 2020 年，OpenAI 推出 GPT-3 模型 ¹³，擁有 1,750 億個參數，是當時最大的語言模型。 2022 年，基於 GPT-3.5 的全能聊天機器人 ChatGPT 推出，能夠完成多種生成式任務（如寫文章、角色扮演等），讓各種應用如雨後春筍般蓬勃發展。

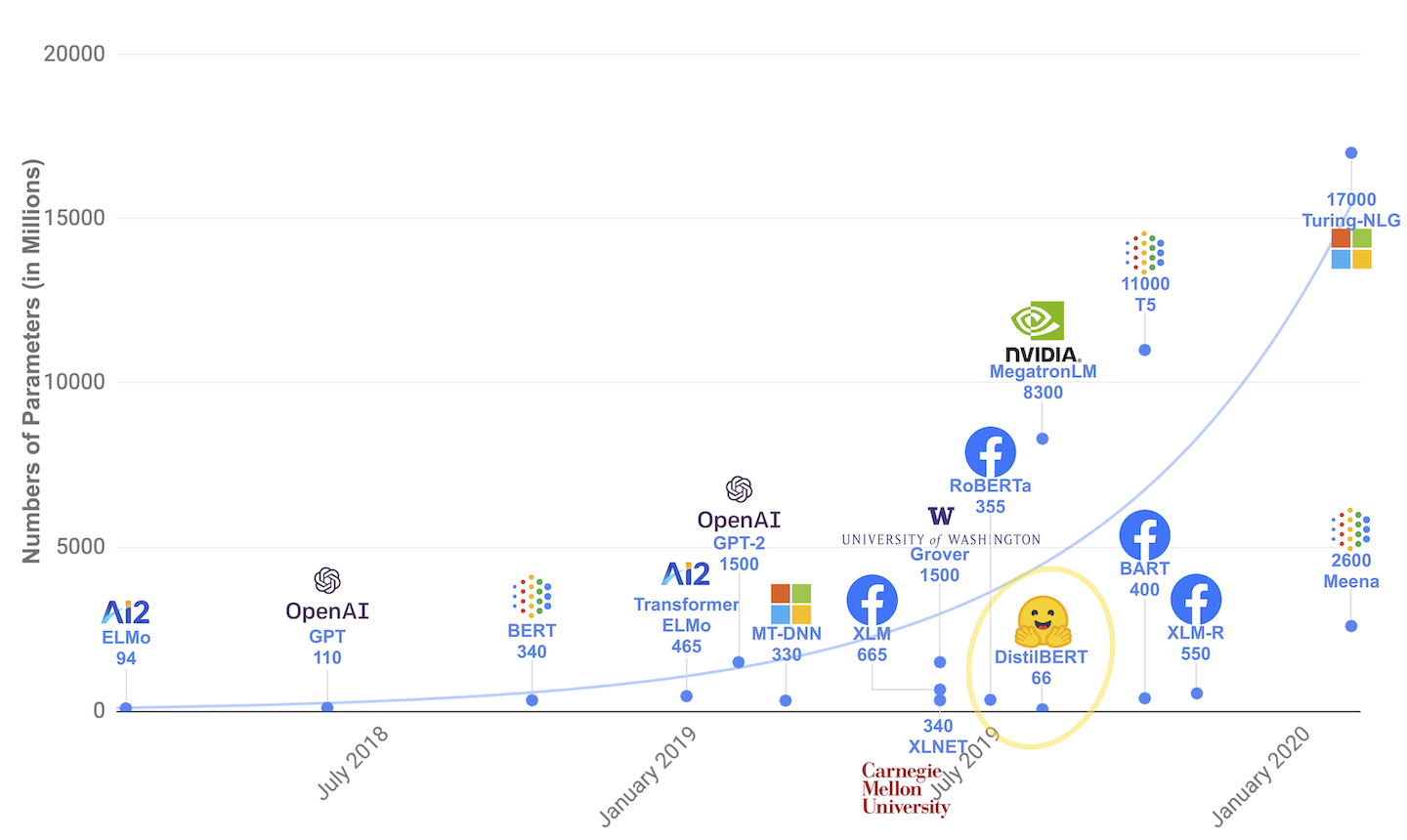
除了少數 outliers (eg. DistilBERT)，語言模型的參數量自 Transformer 發表後開始以一年 10 倍的速度暴漲 ¹⁴

時至今日，深度學習已經成為 AI 的主流技術。這些龐大的模型又被稱作大型語言模型 (large language model, LLM)，能夠將文字、影音等資訊轉換至向量空間，經過海量參數的運算與思考後，再轉化成各種輸出。這種模型又被稱作 multimodal model，宛如給傳統的 CNN 裝上大腦，使其能夠與語言互動。有了大型語言模型作為大腦，只要再給予感官和手腳，AI 就能充分運用至各個領域。例如接受 IoT 設備的感測訊號來建立智慧工廠、接受影像與紅外線訊號來建立自動駕駛、連結至電腦終端來建立伺服器、連結至機械四肢來建立機器人。藉由 AI agent，各種軟硬體開始蓬勃發展，人工智慧也從學術領域落地至商業應用。

2024 年，諾貝爾物理學獎頒給 John Hopfield 與 Geoffrey Hinton，表彰其對神經網路的貢獻 ¹⁵。諾貝爾化學獎一半則頒給 Google DeepMind 開發 AlphaFold 的團隊，表彰其對蛋白質結構預測的貢獻；另一半則頒給 David Baker，後者開發出設計蛋白質的程式 Rosetta，並在最新版本引入 diffusion model ¹⁶。

神經網路

那究竟什麼是神經網路呢？為什麼它可以學習出人類難以定義的「規則」？我們需要先回到 1940 年代，也就是單層感知器的時代。所謂的感知器，其實就是模仿生物體的神經元，將輸入的訊號加總起來。一旦訊號的強度超過一定閾值，神經元就會被激活，

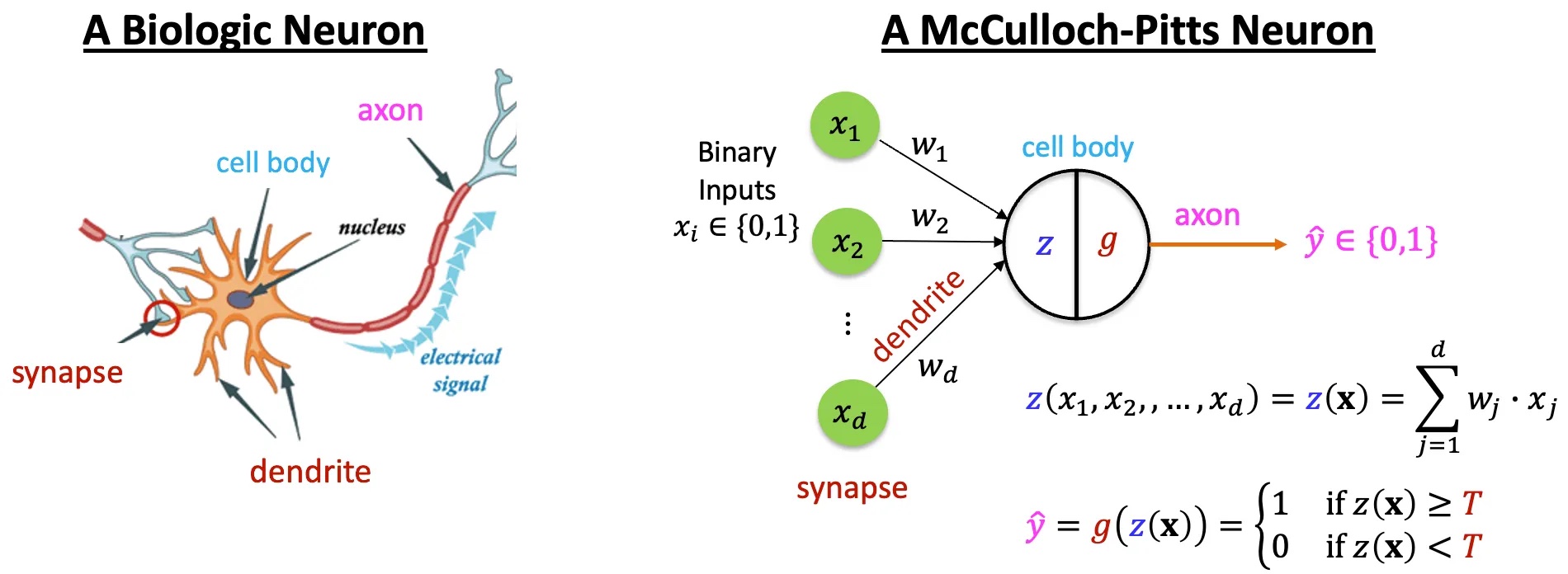
McCulloch-Pitts Neuron Model (1943) ² ¹⁷

從數學上來說，就是將輸入訊號 $x_1 \sim x_d$ 取加權和 $z(x)$ ，再經過激活函數 (activation function) $g(z)$ 來決定是否啟動。上圖右的神經元包含一個典型的激活函數，當 $z(x)$ 大於閾值，輸出為 1；否則輸出為 0。而透過給定訓練資料 (training data) 與正解 (ground truth)，我們可以不斷調整權重 $w_1 \sim w_d$ ，使得模型的預測結果越來越接近正確答案，這種訓練方式又稱為 監督式學習 (supervised learning)。

然而，單靠調整 $w_1 \sim w_d$ 真的可以解決所有問題嗎？答案顯然是否定的。單層感知器只能解決線性可分的問題 (eg. AND, OR)，無法解決 XOR 問題。以下表為例，將 $x_1$ 、 $x_2$ 兩個參數作為輸入，並不存在一條斜直線可以在二維平面上將兩個類別分開；也就是不存在一個通解可以滿足所有輸入與輸出的配對，所以訓練過程永遠無法收斂。

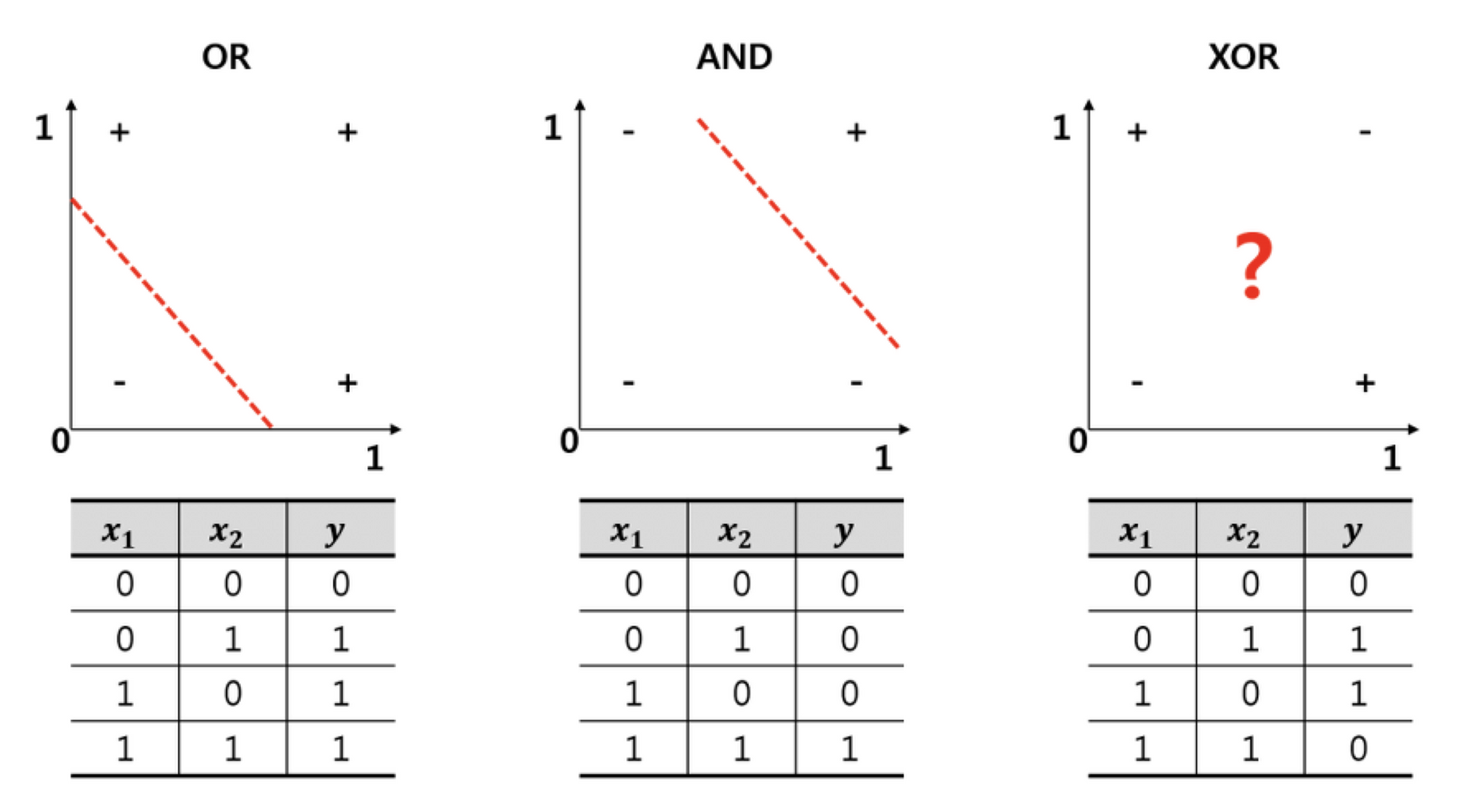
將單顆神經元的訓練結果繪製於二維平面，程式部分可以參考 Github 連結

想要解決這個問題，我們就需要引入多層感知器 (MLP) 的概念。以下面影片為例，當加入第二顆感知器後，我們相當於有第二條斜直線可以逼近 XOR 的解。注意影片中每顆神經元有額外加上 bias，並且使用 sigmoid function $\sigma(x)$ 作為激活函數，這個我們稍後也會介紹到。

理論上，只要我們不斷增加神經元的數量，組成複雜的神經網路，就可以用線性疊加的方式模擬任何函數，解決任何問題。那為什麼這個方法一開始發展不起來呢？因為當模型變得越複雜，要找出正確的權重就變得異常困難和費時。這就像是在汪洋大海中的一葉扁舟，如果沒有可靠的方式（羅盤，或者任何數學性的手段），幾乎不可能抵達目的地。

梯度下降

一種可能的方式是採用梯度下降法 (gradient descent)。回憶一下高中數學，當我們在函數曲線上任一點作微分，即為該點的切線斜率。而斜率等於 0 代表該點為局部最大值或最小值，通常也是我們想要得到的局部最佳解。對於一個多維函數 $f(x_1 \sim x_d)$ ，我們可以對每個變數分別作偏微分，得到的向量稱為梯度 $\nabla f(x_1 \sim x_d)$ ，代表函式在該點最陡的上升方向。

$x = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_d \end{bmatrix},\quad \nabla f(x) = \begin{bmatrix} \frac{\partial f(x)}{\partial x_1} \\ \frac{\partial f(x)}{\partial x_2} \\ \vdots \\ \frac{\partial f(x)}{\partial x_d} \end{bmatrix}$

訓練神經網路的過程中，我們會固定輸入 $x$ 求得輸出 $\hat{y}$ ，然後將其與正確答案 $y$ 比較並計算兩者間誤差。在實際訓練時往往採用批次 (batch) 的方式進行，所以通常會採用平均誤差 (mean squared error, MSE) 作為損失函數 (loss function)： $E = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2$ ，其中 $i$ 代表樣本的 index。

我們希望盡可能最小化這個誤差，也就是找到誤差曲線的全域最小值，這時就可以採用梯度下降法。將當前權重減去其梯度的方向，這樣就能夠朝著誤差最小的方向前進。

$w_{t+1} = w_t - \eta \cdot \nabla E(w_t)$

其中 $t$ 代表目前的訓練次數， $\eta$ 則代表 學習率 (learning rate)，也就是每次更新 $\nabla E$ 的幅度。學習率的選擇堪稱藝術，太大會導致錯過最小值，太小則會導致收斂速度過慢。所以比較好的作法是在訓練初期選擇較大的學習率，並隨著訓練次數的增加逐漸減小，這樣就能夠在初期快速收斂，後期精確調整。這種方式又稱作 adaptive gradient descent (AdaGrad) ¹⁸。

類似的作法還有引入動量 (momentum) 的概念，就像一顆球從山坡滾下時會持續累積動量，這樣更有機會逃脫局部最小值，進而找到真正的全域最小值。目前最常見的方式是 adaptive momentum (Adam) ¹⁹，結合了自適應學習率與動量的概念。這些促進訓練效率的演算法又稱作 優化器 (optimizer)。

optimizers on saddle point ²⁰

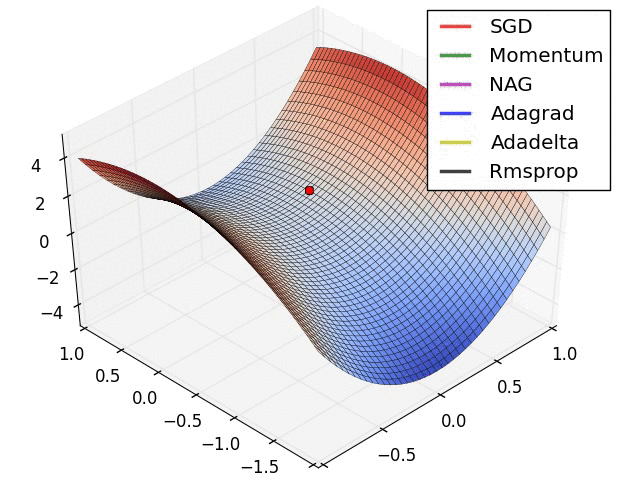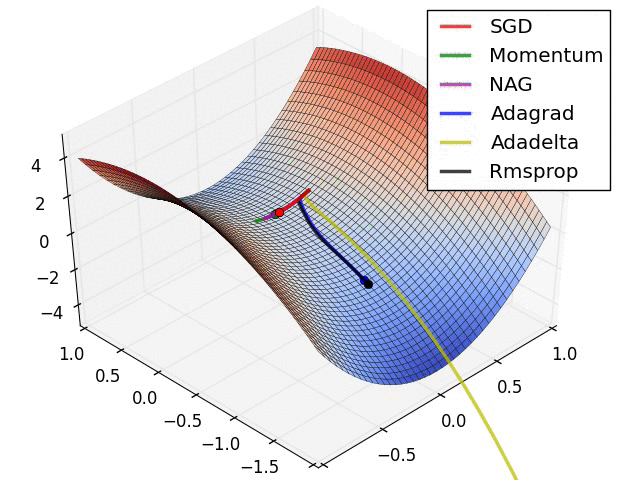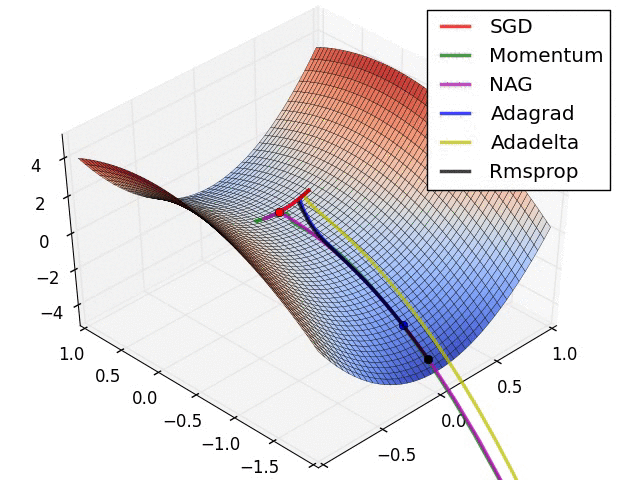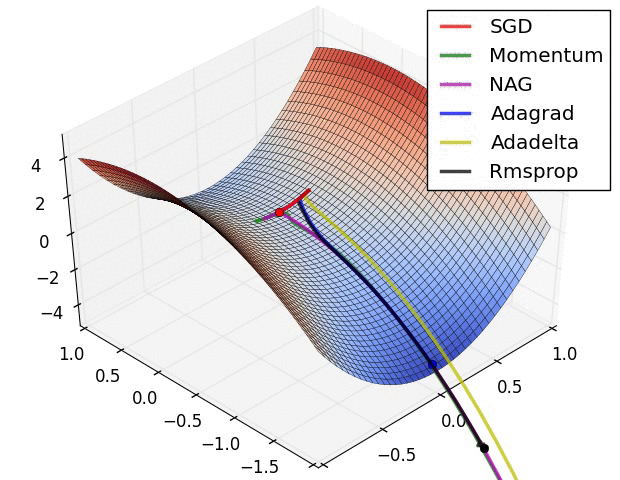
除了關注優化器，我們還需要注意激活函數的選擇。傳統的激活函數可以是一個 sign function，然而為了計算導數，我們必須確保該函數在每一點皆可微分，也就是必須為一個連續曲線。常見的激活函數有 tanh function 和 sigmoid ( $\sigma$ ) function，兩者主要差在輸出範圍是 $[-1, 1]$ 或 $[0, 1]$ 。

激活函數： $tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}},\quad \sigma(x) = \frac{1}{1 + e^{-x}}$

函數導數： $tanh'(x) = 1 - tanh^2(x),\quad \sigma'(x) = \sigma(x)(1 - \sigma(x))$

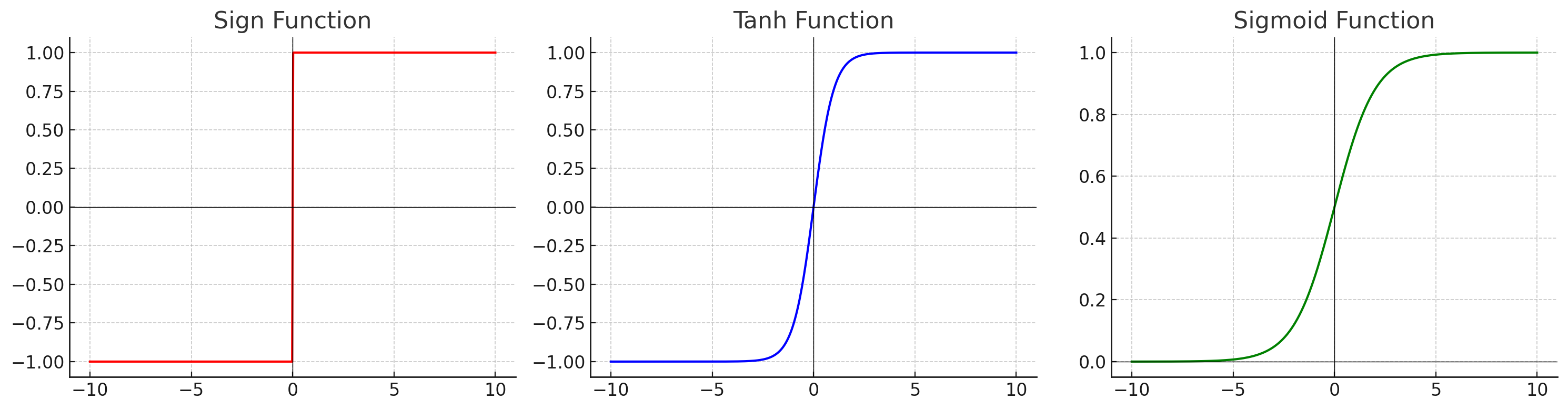
有了以上知識後，我們就可以開始計算神經網路的輸出與損失了。

反向傳播

首先考慮以下神經網路，包含 $X_1$ 、 $X_2$ 兩個輸入項，以及 $G$ 、 $F$ 兩顆神經元和其對應的 bias 輸入項。神經元 $F$ 的輸出即為預測值 $\hat{y}$ ，我們會與正解 $y$ 透過損失函數 $E$ 進行比對後計算出損失值 $e$ 。

一個簡單的雙層神經網路示意圖

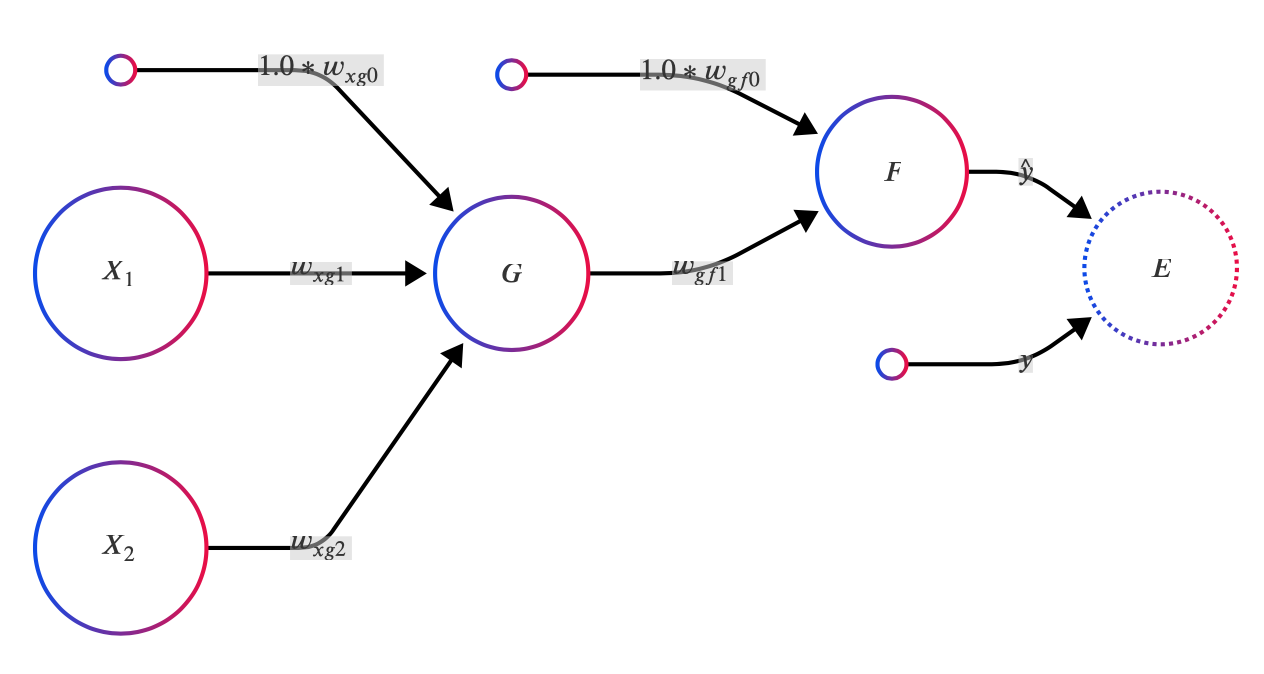
為了方便展示，我們讓神經元 $G$ 使用 tanh 作為其激活函數， $F$ 使用 sigmoid 作為激活函數。 $F$ 使用 sigmoid 的好處是可以將輸出結果正規化到 [0, 1] 範圍，適合用來預測機率。整個神經網路的輸出可以整理成以下合成函數：

$\hat{y} = F \circ G = \sigma(w_{gf0} + w_{gf1} \cdot tanh(w_{xg0} + w_{xg1} \cdot X_1 + w_{xg2} \cdot X_2))$

若我們假設訓練資料只有一筆 (n=1)，且使用 MSE 作為損失函數，帶入上述公式整理後如下所示：

$loss = (y - \hat{y})^2 = (y-\sigma(w_{gf0} + w_{gf1} \cdot tanh(w_{xg0} + w_{xg1} \cdot X_1 + w_{xg2} \cdot X_2)))^2$

進一步以合成函數表示如下（方便等下展示梯度計算）：

$loss = e \circ f \circ z_f \circ g \circ z_g$

$where \; e = (y-f)^2, f = \sigma, z_f = w_{gf0} + w_{gf1} \cdot g, g = tanh, z_g = w_{xg0} + w_{xg1} \cdot X_1 + w_{xg2} \cdot X_2$

接著我們開始計算損失函數的梯度 $\nabla E$ 。套用連鎖率 (chain rule)，我們可以將損失值對五個權重的偏微分寫成萊布尼茲表示法，並進一步整理成各神經元的損失函數 (eg. $loss \; F$ 、 $loss \; G$ )：

$\frac{\partial e}{\partial w_{gf0}} = \frac{\partial e}{\partial f} \cdot \frac{\partial f}{\partial z_f} \cdot \frac{\partial z_f}{\partial w_{gf0}} = -(y-f) \cdot \sigma '(z_f) \cdot 1 = loss \; F \cdot 1$

$\frac{\partial e}{\partial w_{gf1}} = \frac{\partial e}{\partial f} \cdot \frac{\partial f}{\partial z_f} \cdot \frac{\partial z_f}{\partial w_{gf1}} = -(y-f) \cdot \sigma '(z_f) \cdot g = loss \; F \cdot g$

$\frac{\partial e}{\partial w_{xg0}} = \frac{\partial e}{\partial f} \cdot \frac{\partial f}{\partial z_f} \cdot \frac{\partial z_f}{\partial g} \cdot \frac{\partial g}{\partial z_g} \cdot \frac{\partial z_g}{\partial w_{xg0}} = -(y-f) \cdot \sigma '(z_f) \cdot w_{gf1} \cdot tanh'(z_g) \cdot 1 = loss \; G \cdot 1$

$\frac{\partial e}{\partial w_{xg1}} = \frac{\partial e}{\partial f} \cdot \frac{\partial f}{\partial z_f} \cdot \frac{\partial z_f}{\partial g} \cdot \frac{\partial g}{\partial z_g} \cdot \frac{\partial z_g}{\partial w_{xg1}} = -(y-f) \cdot \sigma '(z_f) \cdot w_{gf1} \cdot tanh'(z_g) \cdot X_1 = loss \; G \cdot X_1$

$\frac{\partial e}{\partial w_{xg2}} = \frac{\partial e}{\partial f} \cdot \frac{\partial f}{\partial z_f} \cdot \frac{\partial z_f}{\partial g} \cdot \frac{\partial g}{\partial z_g} \cdot \frac{\partial z_g}{\partial w_{xg2}} = -(y-f) \cdot \sigma '(z_f) \cdot w_{gf1} \cdot tanh'(z_g) \cdot X_2 = loss \; G \cdot X_2$

上述公式看得頭昏腦脹？沒關係，我們可以整理成兩個重點：

損失函數對各權重的偏微分 = 該神經元 loss * 各權重對應的輸入
該神經元 loss = 後一層神經元 loss * 神經元間的權重 * 該神經元激活函數的導數

例如 $loss \; G = loss \; F \cdot w_{gf1} \cdot tanh'$ ，我們不難發現其中很多項都是與後一層神經元共用的。這種計算梯度的方式，可以從最後一顆神經元一路往回推算到每個權重，這就是 反向傳播 (back propagation)。反向傳播簡化了原本複雜的神經網路梯度計算，只需要計算激活函數的導數後，將輸入值與權重逐項帶入就好。最終訓練權重的調整公式如下所示：

$\Delta w_{gf0} = -\eta \cdot loss \; F \cdot 1$

$\Delta w_{gf1} = -\eta \cdot loss \; F \cdot g$

$\Delta w_{xg0} = -\eta \cdot loss \; G \cdot 1$

$\Delta w_{xg1} = -\eta \cdot loss \; G \cdot X_1$

$\Delta w_{xg2} = -\eta \cdot loss \; G \cdot X_2$

模型訓練

截至目前為止，我們已經介紹何為神經網路、如何將輸入訊號激活為輸出結果、以及如何訓練神經網路的權重。但我們還沒有真正將神經網路應用到實際問題上，所以本章節就要來實作一個最經典的 MNIST 手寫數字辨識模型。

MNIST 資料集 (Modified National Institute of Standards and Technology database) 是一個源自美國國家標準技術研究所的手寫數字資料庫，包含 60,000 筆訓練資料和 10,000 筆測試資料，皆標準化為 28*28 pixel 的黑白圖片，方便訓練與測試模型。

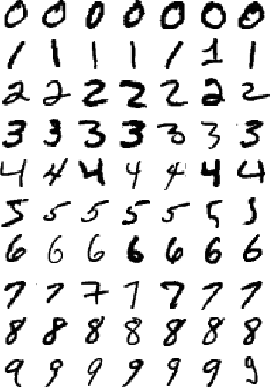
(左) MNIST 資料集範例 (右) 1989 年楊立昆展示如何透過 LeNet-1 辨識手寫數字

在這個章節中，我們將使用 Google Tensorflow 的高階函式庫 Keras 來實作神經網路。 Keras 原先為一個獨立 Python API，因其兼容 Tensorflow 後端，在 2019 年被 Tensorflow 2.0 正式合併為核心模組之一。與 Tensorflow 類似的還有 Meta 開發的 Pytorch，這兩個是目前最廣泛被使用的深度學習框架，其差別可以參考這篇文章。

以下程式碼可以參考我的 Github，若沒有 GPU 環境建議可以在 Google Colab 上選擇 runtime 為 T4 GPU 後運行，這會比直接使用 CPU 訓練快很多。我們首先載入 tensorflow 與 keras 模組，並設定訓練總週期 (epoch) 為 20，代表會將全部的訓練資料重複跑過 20 次。接著設定批次 (batch size) 為 1，代表每批只用一筆資料做訓練。

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.utils import to_categorical
import numpy as np
import logging
tf.get_logger().setLevel(logging.ERROR)

EPOCHS = 20
BATCH_SIZE = 1

接著我們透過 keras 模組直接下載 MNIST 資料集，會產生 60,000 筆訓練資料和 10,000 筆測試資料，皆包含圖片與標籤。每張圖片會是 28*28 個 uint8 數值 (0-255) 的陣列，標籤則是紀錄 0-9 的答案。下載完成後，我們還需要將圖片陣列從 0-255 標準化至 0-1，這是為了將推論與訓練過程的輸出控制在 0-1 附近，避免激活函數因為過大的輸入而飽和 (saturation)，這個議題我們稍後再談。

接著，我們需要將標籤做 one-hot 編碼，也就是將數值映射到 0-9 的稀疏空間。例如：

$one-hot(1) = [0,1,0,0,0,0,0,0,0,0]$

$one-hot(3) = [0,0,0,1,0,0,0,0,0,0]$

$one-hot(9) = [0,0,0,0,0,0,0,0,0,1]$

因為這是一個「分類問題」而不是「回歸問題」，也就是數字 0-9 之間並沒有順序關係。例如對於正解 3，如果模型預測 2.9，你或許還可以透過四捨五入來推測是 3。如果模型預測 2.5 呢？那是否代表它認為 2 或 3 皆有 50% 可能？如果某張圖片很像 3 或 5 導致模型預測出 4 呢？要如何判斷它是真的認為 4，還是同時猜測 3、5，或甚至 2、6？為了避免這個問題，我們習慣將分類標籤投影到陣列中作個別的機率預測，以避免類別之間過度耦合。上述過程撰寫如下：

# 載入訓練資料集與測試資料集
mnist = keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

# 替樣本做標準化  (standardization)
mean = np.mean(train_images)
stddev = np.std(train_images)
train_images = (train_images - mean) / stddev
test_images = (test_images - mean) / stddev

# 替標籤做 one-hot 編碼
train_labels = to_categorical(train_labels, num_classes=10)
test_labels = to_categorical(test_labels, num_classes=10)

接著我們可以使用 keras.Sequential() 來建立一個最基本的序向模型。在下面的架構中，我們先透過 Flatten() 層將圖片從 28*28 的 2D-array 展平成長度 784 的 1D-array。接著我們建立兩個密集層 (dense layer)，又稱作「全連接層」，因為它會把輸入全部接到該層所有神經元中，是神經網路的核心。以下面為例，兩個密集層各含 25、10 顆神經元，分別用 $tanh()$ 與 $sigmoid()$ 作為激活函數。 Sigmoid 函數的優點先前有提過，因為其輸出範圍剛好在 [0, 1]，很適合用來預測機率分佈（也就是作為分類問題的輸出）。在這邊我們設定 10 顆神經元作為輸出，剛好可以對應上 one-hot 標籤 0-9 的陣列索引。另外，我們還設定了範圍 -0.1 ~ 0.1 的隨機均勻初始化 (random uniform) 作為權重初始值，避免其在初期訓練時過度偏向某些權重，同時也避免過大或過小的權重造成輸出飽和。

initializer = keras.initializers.RandomUniform(minval=-0.1, maxval=0.1)
model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(25, activation='tanh',
                       kernel_initializer=initializer,
                       bias_initializer='zeros'),
    keras.layers.Dense(10, activation='sigmoid',
                       kernel_initializer=initializer,
                       bias_initializer='zeros')])
model.summary()

透過 summary() 我們可以查看目前模型的整體架構與參數量，可見有 19,885 個參數要訓練：

Model: "sequential"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ flatten (Flatten)               │ (None, 784)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense (Dense)                   │ (None, 25)             │        19,625 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_1 (Dense)                 │ (None, 10)             │           260 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
 Total params: 19,885 (77.68 KB)
 Trainable params: 19,885 (77.68 KB)
 Non-trainable params: 0 (0.00 B)

接著我們著手設定優化器，這邊使用隨機梯度下降法（SGD），也就是每經過一筆資料就更新權重，並且設定學習率為 0.01，使用 MSE 作為 loss function。隨著 batch size 的提升，訓練的穩定性通常會跟著提升（因為一次看到的資料更多，避免收斂方向偏誤），但是會需要更多 GPU memory 來讀入資料。我們將此模型編譯 (compile) 過後，就可以開始進行訓練，也就是將權重與資料進行擬合 (fit)。

opt = keras.optimizers.SGD(learning_rate=0.01)

model.compile(loss='mean_squared_error', optimizer = opt,
              metrics =['accuracy'])

history = model.fit(train_images, train_labels,
                    validation_data=(test_images, test_labels),
                    epochs=EPOCHS, batch_size=BATCH_SIZE,
                    verbose=2, shuffle=True)

輸出結果如下，等待一段時間後，就可以完成模型訓練。

Epoch 1/20
60000/60000 - 139s - 2ms/step - accuracy: 0.6952 - loss: 0.0523 - val_accuracy: 0.8807 - val_loss: 0.0272
Epoch 2/20
60000/60000 - 140s - 2ms/step - accuracy: 0.8928 - loss: 0.0219 - val_accuracy: 0.9121 - val_loss: 0.0178
Epoch 3/20
60000/60000 - 142s - 2ms/step - accuracy: 0.9127 - loss: 0.0167 - val_accuracy: 0.9164 - val_loss: 0.0154

...

Epoch 19/20
60000/60000 - 145s - 2ms/step - accuracy: 0.9504 - loss: 0.0089 - val_accuracy: 0.9398 - val_loss: 0.0101
Epoch 20/20
60000/60000 - 144s - 2ms/step - accuracy: 0.9519 - loss: 0.0087 - val_accuracy: 0.9413 - val_loss: 0.0098

我們可以透過 matplotlib 將訓練過程作圖，或使用 TensorBoard 等套件直接進行資料視覺化。圖中可以發現 training loss 從 0.05 逐步下降到 0.01，training accuracy 也從 0.7 上升到 0.95。在測試資料的部分，儘管略不及訓練資料，但也同步下降 loss 與提升 accuracy，代表整個訓練過程是成功的。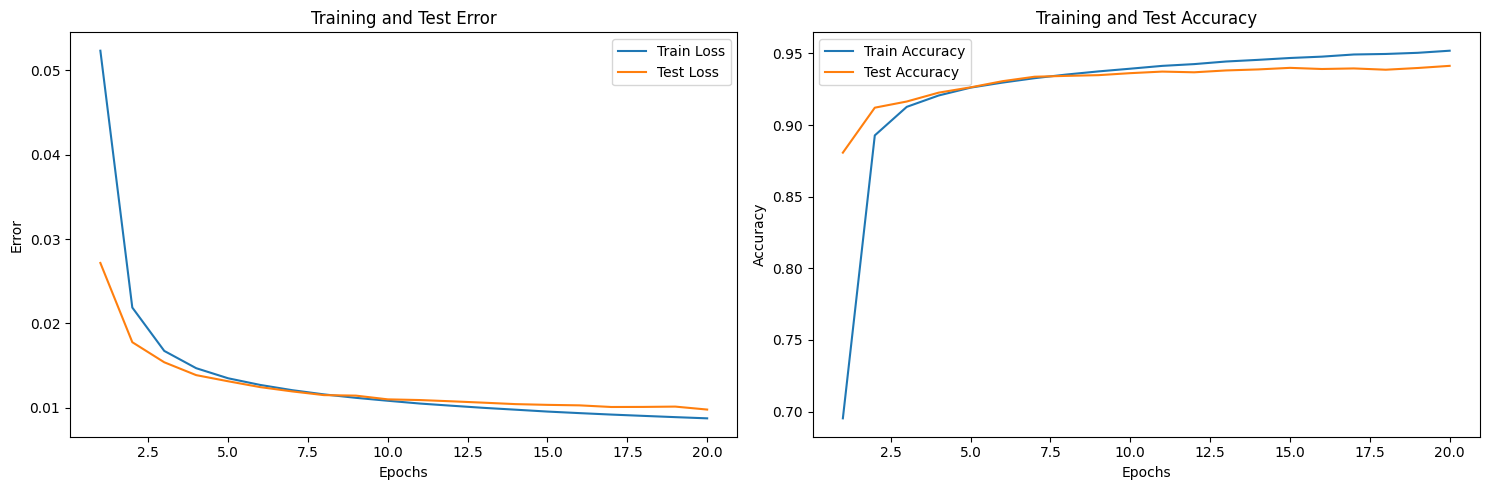

若我們將訓練完的模型，拿前五筆測試資料進行預測，可以看到模型經過最終 10 顆神經元的 sigmoid 函數後，會分別對 10 種類別進行預測，輸出一個介於 0-1 的機率陣列。我們一樣可以將預測結果視覺化，並取機率最高的標籤作為預測值。

model.predict(test_images[:5])

array([[2.3932243e-03, 2.3173345e-03, 2.8411698e-02, 3.4776039e-02,
        4.2185368e-04, 4.0405830e-05, 8.8253018e-04, 9.9372983e-01,
        2.6027383e-03, 8.7425479e-04],
        ...
    ], dtype=float32)

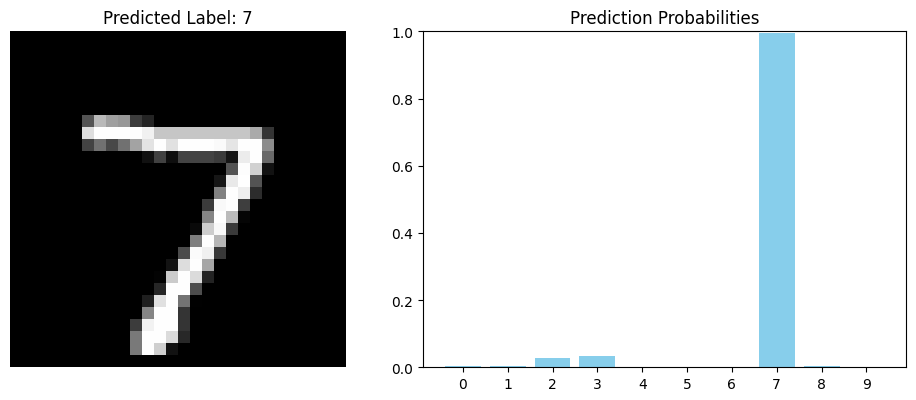
最後，我們可以將訓練好的模型儲存成 HDF5 格式，未來可以直接將模型載入，就不需要重新訓練。下面可見新模型的評估結果跟先前訓練好的模型準確度基本一致。

model.save('model.h5')

new_model = keras.models.load_model('model.h5')
loss, acc = new_model.evaluate(test_images, test_labels, verbose=2)

313/313 - 1s - 4ms/step - accuracy: 0.9413 - loss: 0.0098

模型改善

神經元飽和

儘管這個範例所訓練的模型已經具備 94% 的 accuracy，但對於更困難的問題或更複雜的模型，我們往往無法這麼順利的收斂。一個可能的原因即是神經元飽和 (neuron saturation)。還記得我們先前展示過 $tanh()$ 與 $sigmoid()$ 的圖形，當輸入超過 [-5,5] 的範圍後輸出就幾乎變成水平，這代表其微分結果逼近 0。而計算神經元 loss 值有一項是激活函數的導數，所以當它變成 0 後， $\Delta w$ 就幾乎不會再更新了，這種現象又稱作 梯度消失 (vanishing gradient)。

一種解法是將輸入資料正規化 (normalization)，例如我們先前提到將圖片數值壓縮到 0-1 範圍。但我們不難發現這樣只能確保模型在第一層不會飽和，卻無法保證中間每一層不會飽和。比較常見的作法是在密集層之間加入 batch normalization layer，每次都將輸出做批次正規化。

keras.layers.Dense(25, activation='tanh')
keras.layers.BatchNormalization()

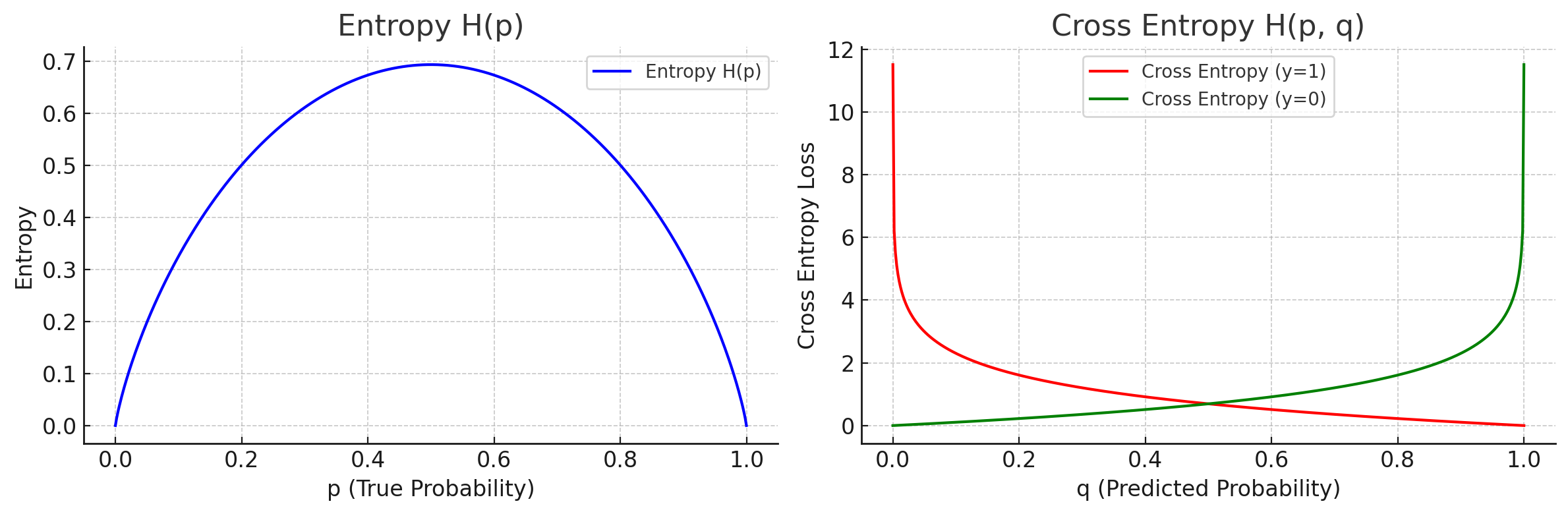
稍早提過的權重初始化方式也是一種改善方向，可以避免在初期因為隨機因素造成特定權重過高導致輸出飽和。另一個方式是直接更換激活函數，例如 $ReLU = max(0,x)$ ，當 x > 0 時輸入與輸出的斜率為固定值，避免因輸入過大而飽和。此外也可以更換損失函數，我們可以將 MSE 改成 MAE (mean-absolute error)，也就是將平方改成絕對值，避免損失項過大導致無法從最後一層傳遞回去，但是收斂速度與穩定度就會受到影響。對於分類問題，我們有一個更適合的損失函數 Cross Entropy：

$H(y, \hat{y}) = \displaystyle\sum_{i} -y_i log(\hat{y_i})$

其中 $y$ 代表正解向量，例如 $[0, 0, 1, 0]$ ； $\hat{y}$ 代表模型預測的機率，例如 $[0.1, 0.2, 0.6, 0.1]$ 。所謂 entropy (熵) 代表所有資訊的「亂度」，當熵越大，代表模型越難預測，或是預測結果越不準確。我們可以回頭去看 Shannon entropy 的定義：

$H(x) = \displaystyle\sum_{i=1}^{N} -p_ilog_2(p_i)$

當預測正確率 0.99，失敗率 0.01 時， $H(x)=-0.99log(0.99)-0.01 log(0.01)= 0.081$ 。
當預測正確率 0.6，失敗率 0.4 時， $H(x)=-0.6log(0.6)-0.4 log(0.4)= 0.971$ 。
當預測正確率與失敗率都是 0.5 時（完全猜不準）， $H(x)=1$ 。

換句話說，預測的不確定性越高，熵就越高。而 Cross Entropy 修改了 log 前那一項為 binary indicator (0 or 1)，讓模型只關注目標類別的機率，其他類別的 entropy 都會變成 0。這麼做可以讓模型往「正確」的方向收斂，而不單只是往「最低亂度」收斂。結果如下圖右，將所有資料的正解（紅色 y=1）上的點加總，就是 Cross Entropy 的和。

另外，在先前的範例程式中，我們使用十顆神經元搭配 $sigmoid()$ 激活函數作為輸出，其隱藏的風險是預測機率的總和不一定為 1。因為每顆神經元都獨立預測，可能會出現諸如 $[0.8, 0.1, 0.6]$ 這種預測結果，不符合物理上的直覺。 $Softmax()$ 可以將輸出向量正規化，例如 $[0.7, 0.1, 0.2]$ ，特別適合多類別預測。

$Softmax(x_i) = \frac{e^{x_i}}{\sum_{i=1}^{N} e^{x_i}}$

從實際案例來看，若我們今天要預測的為回歸 (regression) 問題，例如明天股票的收盤價，就適合用 MSE 或 MAE 作為損失函數來計算數值差異。若今天要預測的是二元分類問題，例如明天股票的漲跌，就適合用 sigmoid + binary cross-entropy。若今天是多元分類問題，例如辨識物體或明天哪隻股票漲最多，就適合用 softmax + categorical cross-entropy。

過度擬合

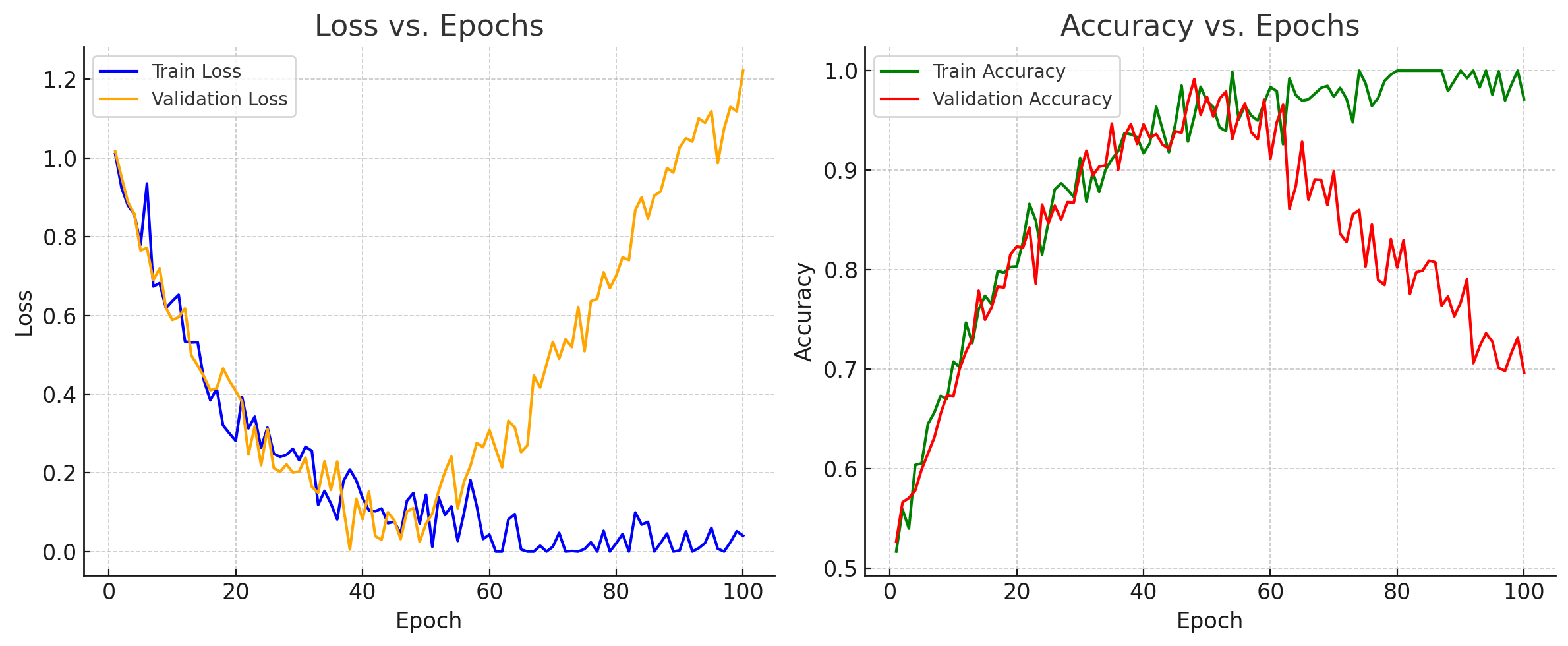
有時候，當我們持續訓練模型的過程中，明明 training loss 持續下降， validation loss 卻遲遲無法下降，甚至開始上升，導致 accuracy 跟著下跌，這種現象又稱作 過度擬合 (overfitting)。過度擬合代表模型開始鑽牛角尖的去 fit 你的訓練資料，導致對新資料的能力無法泛化。這很可能是因為訓練資料集有某種明確特徵被抓出來，但是這個特徵並不通用於實際標準，導致模型學過頭「學錯了」。

要解決 overfitting，最直觀的辦法就是在 validation loss 開始上升前停止訓練，又稱作 early stopping。在 tensorflow 中可以使用 callback function 來設定 early stopping 跟自動儲存權重的策略。

from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint

# 監控 val_loss，如果連續 5 次沒改善就停止
early_stop = EarlyStopping(
    monitor='val_loss',
    patience=5,
    restore_best_weights=True  # 回復最佳權重
)

# 每次 val_loss 最好時儲存模型
checkpoint = ModelCheckpoint(
    filepath='best_model.h5',
    monitor='val_loss',
    save_best_only=True,
    save_weights_only=False
)

model.fit(train_images, train_labels,
    validation_data=(test_images, test_labels),
    epochs=EPOCHS, batch_size=BATCH_SIZE,
    callbacks=[early_stop, checkpoint])

另一種技巧是 權重衰減 (weight decay)，也就是在損失函數加上某個與權重有關的懲罰項 (penalty)，限制權重的範圍來增加模型的普適性。常見的有 L1 regularization 和 L2 regularization，前者使用權重絕對值，後者使用權重平方項。這類作法可以壓低無用的權重，簡化模型的複雜度。

L1 penalty: $\lambda \sum_{i=1}^{N} | w_i |$

L2 penalty: $\lambda \sum_{i=1}^{N} w_{i}^{2}$

下圖是在 Tensorflow Playground 搭配 L1 regularization 來訓練模型，可以發現不重要的權重都衰減至逼近 0，推薦自己操作看看。數學原理牽涉到拉格朗日乘數法，可以參考這篇文章，礙於篇幅就不贅述。

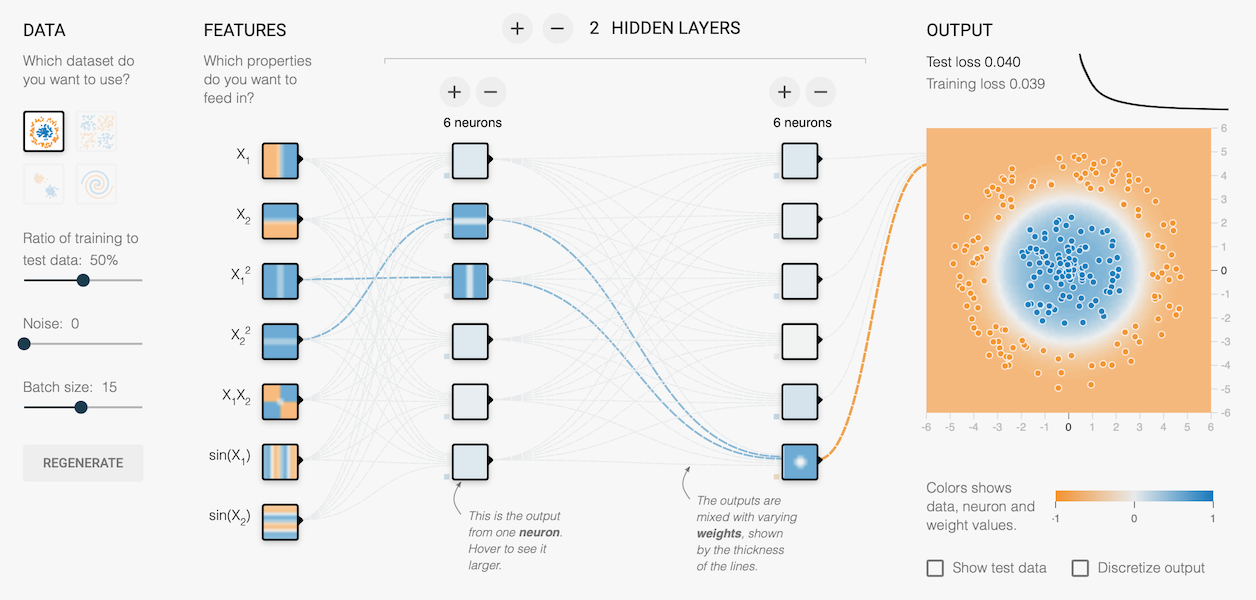
既然提到權重衰減，那就不得不提到 丟棄法 (dropout) ²¹。 Dropout 的概念是在每個 batch 的訓練週期中，隨機移除特定比例的神經元 (eg. 20%)，以避免模型依賴特定權重來學習特徵。這個作法與權重衰減的概念正好相反，卻可以非常有效的減少 overfitting，只需要在建構模型時增加 dropout layer 即可。

keras.layers.Dense(25, activation='tanh')
keras.layers.Dropout(0.2)

以上方法都是從模型角度來治標，若要治本，更根本的解決手段是增加豐富的訓練資料來涵蓋所有特徵。我們在進行資料前處理與分割時，就應該充分思考資料是否足夠具備普適性。例如對於 MNIST 資料集，不同的明度、文字位置與方向是否對模型判斷造成影響？可以利用 資料擴增法 (data augmentation)，透過一些翻轉、縮放等手段來主動增加訓練資料，拓展資料的泛性。

最後，我們自己準備的資料可能不夠多元。可以直接使用網路上已經先用大量資料訓練過的成功模型，再套用至我們的資料後進一步作訓練。即便不是相同的分類問題，也經常有較好的學習效果，這種方式又叫做 遷移式學習 (transfer learning)。遷移式學習被廣泛使用在目前的主流應用中，特別是對於將來會講到的大型語言模型來說非常重要。因為從頭訓練模型相當困難，能夠站在巨人的肩膀上拓展視野，是科學邁進的重要方式。

總結

建立基於神經網路的模型是目前人工智慧的主流手法，透過明確的定義問題，我們可以靠著正確的輸入與輸出尋找資料之間的關係，並將其記錄在模型權重裡。這種學習方式特別適合難以條列規則的使用場景，例如感知問題、生成式問題等，能夠廣泛普及到各個領域。

若要透過深度學習來解決問題，一般來說我會優先搜尋網路上是否已經有現成的模型可以直接使用，例如 Kaggle、Hugging Face 都是目前很大的開源模型庫，同時兼具資料集與社群的功能。如果有特殊需求要自行訓練，我也建議從現有的模型與權重開始著手，通常資料與文件較齊全，比較容易成功。

決定訓練模型後，我們必須根據定義的問題來蒐集相關資料，並確保資料的品質能提供足夠的資訊來預測結果。取得資料後也需要考慮一些常見的前處理手段，例如標準化、向量化、缺漏值處理、特徵工程、資料擴增等等。若要從頭開發模型，則建議先從架構比較簡單的模型著手，確定其有著超過 baseline 的預測能力，再開始逐步增加神經元的數量。在加大模型的過程中，很可能發生難以收斂或 overfitting 等現象，需要透過一些諸如 dropout、regularization 等手段來慢慢排除。

在調教模型的過程中，我們往往需要不斷測試架構，例如激活函數、損失函數、優化器，或是超參數 (hyperparameter) 如 epoch、batch size、learning rate 等。可以將模型調教當成一種搜尋問題，建立搜尋空間後不斷自動化測試，配合基因演算法 (genetic algorithm) 等方式探索最佳組合。最後，我們不要忘記即時儲存最佳權重，多次迭代後就能慢慢找到解決問題的手感。

有了基礎知識後，接下來幾個章節我們將會個別探討目前市面上的主流模型與作法，如 CNN、RNN、Transformer 等架構。

Next: DL 二部曲: to See (待更新)

Alan Mathison Turing. "On computable numbers, with an application to the Entscheidungsproblem." J. of Math 58.345-363 (1936): 5. ↩
Warren S. McCulloch, and Walter Pitts. "A logical calculus of the ideas immanent in nervous activity." The bulletin of mathematical biophysics 5 (1943): 115-133. ↩ ↩²
Dominique Cardon, et al. "Neurons spike back: The Invention of Inductive Machines and the Artificial Intelligence Controversy." Réseaux : communication, technologie, société, 2018, n° 211 (5), pp.173. ↩
Alan Mathison Turing. "Computing Machinery and Intelligence", Mind, LIX (1950): 433–460. ↩
Rumelhart, David E., Geoffrey E. Hinton, and Ronald J. Williams. "Learning representations by back-propagating errors." Nature 323.6088 (1986): 533-536. ↩
Yann LeCun, et al. "Backpropagation applied to handwritten zip code recognition." Neural computation 1.4 (1989): 541-551. ↩
Yann LeCun, et al. "Gradient-based learning applied to document recognition." Proceedings of the IEEE 86.11 (1998): 2278-2324. ↩ ↩²
Jia Deng, et al. "Imagenet: A large-scale hierarchical image database." 2009 IEEE conference on computer vision and pattern recognition. ↩
Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton. "Imagenet classification with deep convolutional neural networks." Advances in neural information processing systems 25 (2012): 1097-1105. ↩
Christian Szegedy, et al. "Going deeper with convolutions." Proceedings of the IEEE conference on computer vision and pattern recognition. 2015. ↩
Kaiming He, et al. "Deep residual learning for image recognition." Proceedings of the IEEE conference on computer vision and pattern recognition. 2016. ↩
Vaswani, Ashish, et al. "Attention is all you need." Advances in neural information processing systems 30 (2017): 5998-6008. ↩
Tom B. Brown, et al. "Language models are few-shot learners." Advances in neural information processing systems 33 (2020): 1876-1901. ↩
Hugging Face, "How do Transformers work?", URL: https://huggingface.co/learn/nlp-course/chapter1/4 ↩
台灣媒體科技中心 SMCTW, 2024諾貝爾物理獎官方新聞稿全文翻譯 ↩
台灣媒體科技中心 SMCTW, 2024諾貝爾化學獎官方新聞稿全文翻譯 ↩
LM Po, "The Evolution of Artificial Neurons", Medium, URL: https://medium.com/@lmpo/the-evolution-of-artificial-neurons-90619f224f63 ↩
J Duchi, E Hazan, and Y Singer, "Adaptive subgradient methods for online learning and stochastic optimization." Journal of Machine Learning Research 12.7 (2011): 2121-2159. ↩
Diederik P. Kingma, and Jimmy Ba, "Adam: A method for stochastic optimization," arXiv preprint arXiv:1412.6980 (2014). ↩
Sebastian Ruder, "An overview of gradient descent optimization algorithms." URL: https://www.ruder.io/optimizing-gradient-descent/ ↩
Nitish Srivastava, et al. "Dropout: a simple way to prevent neural networks from overfitting." The journal of machine learning research 15.1 (2014): 1929-1958. ↩

目錄

緣起