- Published on
字串搜尋演算法的心得
- Authors

- Name
- Ryan Chung

Intro
以前學演算法時,從沒感受到字串搜尋有什麼重要性。 在過去有限的經驗裡,字串搜尋往往只發生在某些簡單的情境,例如從前端發送的字串裡比對出某些狀態和資訊。 通常要比對的字串與被比對的資料都不長,暴力解一般毫無問題,甚至各語言都有對應的字串搜尋函式,不用深入了解原理也可以順利使用。
但演算法的出現就是為了解決某些問題,一旦碰到才會真的仔細琢磨。 這幾年做基因序列比對的研究,特別是針對高通量定序實驗 (NGS),需要將大量長度不等的 RNA 片段配對回原本的基因體當中。 這可是一件浩大的工程,不僅要比對的短序列極多(數萬到數百萬條),參考的基因體更是極其龐大(數十億)。
某種程度上,可以將上述問題視為一種字串搜尋,只是大數據下時間與空間複雜度勢必變得非常重要,程式跑太久可是會影響研究進度啊。 甚至基因本身還有各種突變、配對區域、定序錯誤等因素需要考慮,讓傳統的字串搜尋問題變得格外複雜。
站在前人的肩膀上總是會想回歸初心,瞭解一下字串搜尋的脈絡。 如果想知道我們在基因比對上到底使用什麼方法,可以直接跳到本章倒數第二節 BWT 演算法。 如果不急就聽我娓娓道來。
String Preprocessing
字串搜尋的問題可以參考 LeetCode 28. Find the Index of the First Occurrence in a String, 基本上就是給定兩個字串,並試圖在長字串 (haystack) 中尋找短字串 (needle) 出現的位置。 在基因比對中,一般將前者稱為 reference 後者稱為 read,這篇文章就讓我沿用這個慣例。
一個簡單的暴力搜尋法如下所示,可以一個個從 reference 中比對每一個 read 字元,一旦不匹配就將 reference index 往後移,直到找到答案 (return i) 或找不到答案 (return -1)。 如果 reference 長度為 n 且 read 長度為 m,時間複雜度就會是 O(mn),空間複雜度視實作方式可能為 O(m) 或 O(1)。
# Python3
def strStr(reference: str, read: str) -> int:
n = len(reference)
m = len(read)
for i in range(n):
if reference[i:i+m] == read:
return i
return -1
在一般字串比對中,這個作法幾乎沒有任何問題。 實際上在原始題目中,測資長度到 104 都能在轉瞬間跑完。 可是一旦 reference 是一篇文章、或是一本書(像是從 word 文件裡做關鍵字搜尋),逐字比對顯然曠日費時。
一種常見的方法是針對 reference 資料做前處理 (preprocess),整理出某些規則來加速後續字串比對的速度。 例如,用一個字典來記錄每個字母出現的位置,考慮以下文章:
abcdefgabc...
可以轉換成新的結構 (0-based index):
dic = {
a: [0,7],
b: [1,8],
c: [2,9],
d: [3],
e: [4],
f: [5],
g: [6],
...
}
這樣如果我們要搜尋字串 abc,就可以直接從 index = 0, 7 開始做比對。 雖然這樣時間複雜度依然是 O(mn),但是當 reference 的分佈足夠平均時(例如用 ASCII 來記錄一篇文章的內容),實際搜尋時間就會逼近除以字典 key 的數量 O(mn/128)。
建立字典本身需要花費 O(n) 的時間與空間,如果需要頻繁比對新字串,這筆交易還是很划算的。 這個例子若放在基因比對中,假設 reference 只存在 ATCG 四種主要鹼基,那比對效率就會提升四倍。
我們可以發現,字典所涵蓋的資訊量其實沒有比原始文章少(他們是可以等效轉換的),只是換個資料結構就可以有不錯的效果。 若是願意犧牲資訊量,就可以得到更大的壓縮效果。 例如 Rabin Karp 演算法就是將原始資料轉換成 hash table,再透過比對 read 的 hash value 來大幅加速。 考慮以下 reference:
235902314152...
若我們想尋找的 read 為 31415 這五位數,可以設定一個長度為五的 sliding window,將原始資料前五位數透過一個適當的 hash function 作轉換。 常見的方法為「取餘數」(例如 mod 13),這樣就可以得到前五位數的 hash value = 23590 % 13 = 8。 接著將 sliding window 往後滑動一格,以此類推建立整個 reference 的 hash table。
reference: "23590"2314152...
2"35902"314152...
23"59023"14152...
| | | ...
hash table: 8,9,3,11,0,1,7,8...
|
read: "31415"
因為 31415 % 13 = 7,所以我們只需經過一次 O(n) 的比對就找到可能的解。 然而實際上,其他五位數也可能取 13 餘數為 7(例如 67399),這即是發生 hash collision。 是故必須進一步比對每個 read 的位元才能確認其是否為答案。 當 hash function 不夠好時,worst-case 依然為 O(mn);但若 hash value 足夠分散,那時間會接近 O(n+m)。
上文是以數字來舉例,實務操作上我們可以將字元轉換成 ASCII 來進行運算與比對。
Prefix & Suffix
重新思考問題,不難發現無論透過何種方式,最佳解一定不可能超過時間複雜度 O(n+m)。 因為我們一定得看過所有 reference 與 read 的內容,才能確認字串在哪個位置。 那有沒有一種演算法可以達成 worst-case 在 O(n+m) 的時間複雜度內完成呢? 這裡就要討論另一種非常重要的比對方式, Knuth–Morris–Pratt (KMP) 演算法。
KMP 演算法一樣可以分成資料前處理和資料比對兩個步驟,不同的是我們前處理的是 read 而不是 reference。 想像一下當我們用暴力解做比對時,一旦發現字元不匹配,就會將 reference index + 1 並重新逐字比對。 然而實際上前幾個字元已經比對過了,根本就不用重看啊! 例如想尋找的 read 為 ABCDABD,當我們比對到最後的 D 發現不合時,代表前面 ABCDAB 與 reference 相匹配,那麼即便 index +1 也絕不可能配對上。
reference: BBCABCDABEABCD...
||||||
read: ABCDABD
比較好的作法應該是直接向後移動 4 位,跳到下一個 A 再來比對。 且剛剛開頭的 AB 我們也已經匹配過,所以直接從第三位 C (也就是 reference 的 E )開始看就行了。
reference: BBCABCDABEABCD...
XXXX||
read: ABCDABD
我們可以發現,這樣只需經過一次 O(n) 的文本掃描就全部看完了,沒有任何冗余的比對。 那麼真正問題是,我們要如何知道可以直接移動 4 位呢? 這就必須解釋如何透過前綴 (prefix) 與後綴 (suffix) 來拆解目標 read 的組成。 假設一個字串為 ABCAB,真前綴 (proper prefix) 代表不包含最後一個字的所有可能前綴。 請直接看範例:
- Prefix: A, AB, ABC, ABCA, ABCAB
- Suffix: ABCAB, BCAB, CAB, AB, B
- Proper Prefix: A, AB, ABC, ABCA (不包含 ABCAB)
- Proper Suffix: BCAB, CAB, AB, B (不包含 ABCAB)
而我們想知道的是每次從前綴開始比對時,是否有跟後綴重複的可能性,也就是下次比對時能否省去中間不重複的部分。 這就必須引入 LPS 的概念,定義如下:
LPS[i] = the longest proper prefix of s[0..i] which is also a suffix of s[0..i].
在 jBoxer 的文章中,又將 LPS 稱作 Partial Match。 採用 proper prefix 的理由也很單純,因為我們只看 substring 而不是原始 string,如果選擇 proper suffix 結果也是一樣。 我們可以計算出每個前綴的 LPS 如下所示:
- A: {} & {A} = {} = 0
- AB: {A} & {AB, B} = {} = 0
- ABC: {A, AB} & {ABC, BC, C} = {} = 0
- ABCA: {A, AB, ABC} & {ABCA, BCA, CA, A} = {A} = 1
- ABCAB: {A, AB, ABC, ABCA} & {ABCAB, BCAB, CAB, AB, B} = {AB} = 2
得到一個與目標字串等長的 LPS 陣列:
| Read | A | B | C | A | B |
|---|---|---|---|---|---|
| LPS | 0 | 0 | 0 | 1 | 2 |
以最後面的 B 為例,他的 LPS 是 2,代表連續與前綴匹配了 2 個位元 (AB),那麼只要移動 3 位(字串長度-LPS)便是要移動的距離。 回到前面的例子,ABCDABD 的 LPS 是 0000120,換句話說當我們發現最後一個 D 不合,代表至少到前一個 B 都是匹配的, 只要將字串位移 len of B (6) - LPS of B (2) = 4,就可以從當下繼續做比對。
# Python3
def KMP(reference: str, read: str) -> int:
lps = [0] * len(read)
# Preprocessing
pre = 0
for i in range(1, len(read)):
while pre > 0 and read[i] != read[pre]:
pre = lps[pre-1]
if read[pre] == read[i]:
pre += 1
lps[i] = pre
# Main algorithm
n = 0 #read index
for i in range(len(reference)):
while n > 0 and read[n] != reference[i]:
n = lps[n-1]
if read[n] == reference[i]:
n += 1
if n == len(read):
return i - n + 1
return -1
Suffix Tree & Array
儘管 KMP 演算法在字串比對中已經非常優秀,他存在一個顯而易見的問題。 因為 preprocess 的對象是 read,每次比對都需要重新迭代一次 reference,造成單次搜尋的效率就是 O(n+m)。 一旦搜尋的次數增加,整體時間就會被 O(n) 給拖累。 例如我開頭提到的高通量基因比對,動輒數百萬次的字串搜尋,儘管每次效率都有 O(n+m),但 reference 長度乘上搜尋次數依然是一個很驚人的數字。 為了解決這個問題,我們可以利用字典樹 (trie) 的資料結構,將 reference 建成一顆後綴樹 (suffix tree)。
以 reference 為 ABCAB 為例,可以分解出下列後綴,並以此建立字典樹(注意 \0 代表此 node 為某個 suffix 的結尾,實作中通常是用布林變數)。
- ABCAB suffix: ABCAB, BCAB, CAB, AB, B
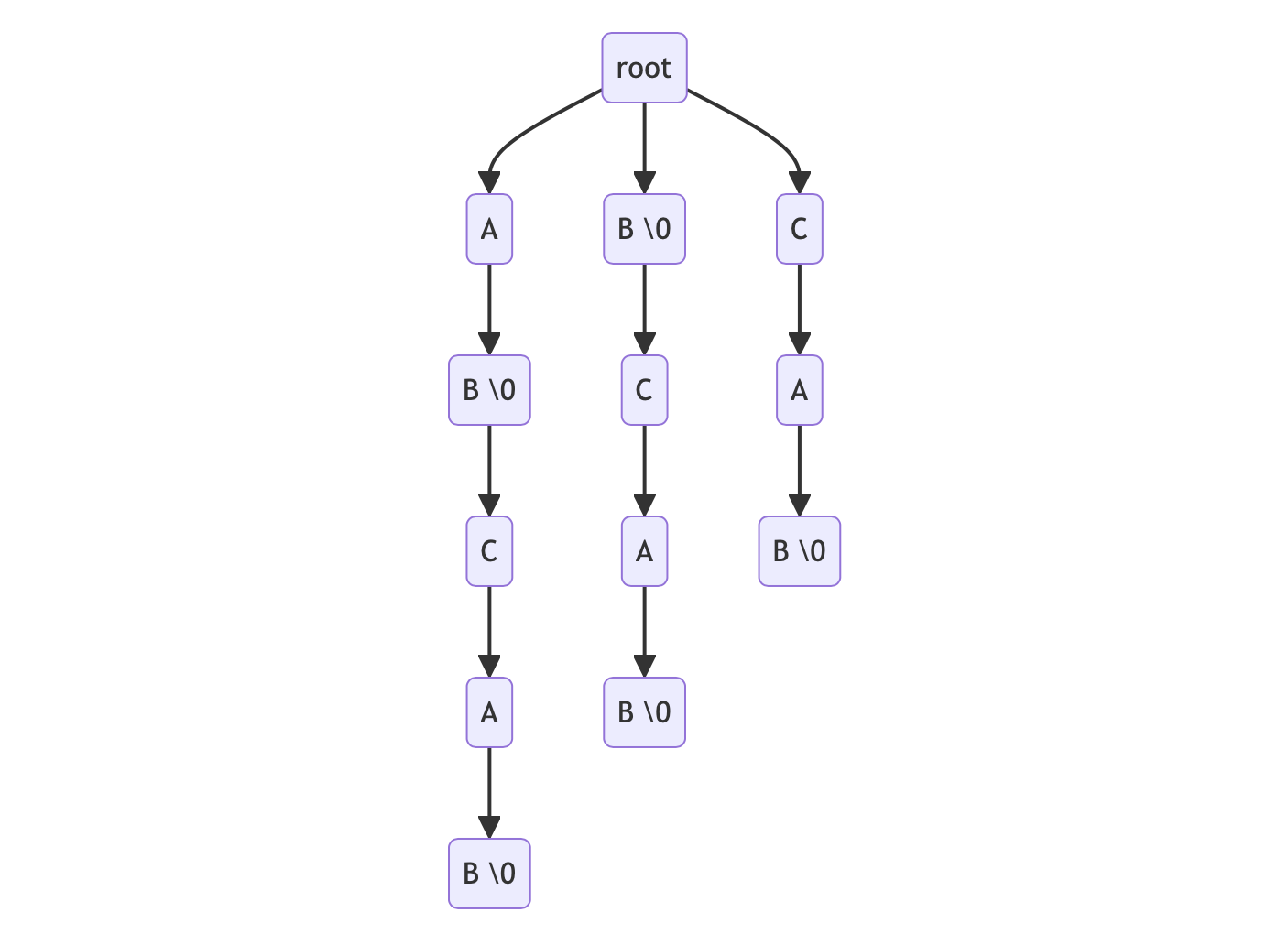
我們只需要在 tree node 中紀錄曾經出現過的 suffix index,就可以在查找字串時一併獲得其位置。 例如我們想尋找的 read 為 BC,指針先移動到第一層 B,再移動到第二層 C,結束搜尋並取得 BCAB 這個 suffix 的 index = 1 (0-based), 這樣單次搜尋的時間複雜度就會大幅降低為 O(m)。
至於建立後綴樹的過程,一般來說需要先將 reference 切割成許多 suffix,再將其插入這棵字典樹,所以時間複雜度會是 O(n2)。 我們可以使用 Ukkonen's algorithm 來優化字典樹的建立過程,時間複雜度會降低至 O(n)。
至此,搜尋效率幾乎已經被最大化,剩下的主要問題是字典樹需要花費很多空間。 考慮在 worst-case 中 reference 每個字元都不相等,意味著每個 suffix 都會串成一條獨立的 linked list,總共會有 n(n+1)/2 個節點,空間複雜度為 O(n2)。 常見的改善方法是將字典樹的路徑壓縮,只保留含分支的節點 (compressed trie)。 例如上面的 root -> C -> A -> B 就可以直接整合成 root -> CAB,刪除大量冗余的節點,空間複雜度會降低至 O(n)。 相關程式和實作細節可以參考 geeks for geeks 上一系列不錯的文章。
儘管後綴樹的時間與空間複雜度看起來很優秀,實作上我們很少會選它。 試想我們每建立一個節點,就包含一份記錄字元索引的陣列。 假設 reference 只包含 [A-Z] 字元,就需要準備 26 個空間來放 next 指針。 如果後綴的內容重複性很高(即陣列每格都有用到),那空間使用率還比較好;如果重複性低,那資料儲存就很稀疏。 換句話說,後綴樹的空間複雜度雖然是 O(n),但是常數倍率卻很大,可能需要 O(26n) 或更大的空間。 另外,節點彼此間用指針在記憶體中相連,對於存取這些不連續的空間也需要消耗更多時間。 對於長度動輒數十億的基因體,需要非常大的記憶體空間才能運算。
另一種比較新的作法是建立後綴陣列 (suffix array or PAT array)。 首先在 reference 後面接上一個 ASCII 比較小的符號 $ 作為終止符(不加也可以,但加了有助於後續步驟的理解), 接著將所有後綴按照內容進行排序,產生新的後綴陣列,代表「每個後綴在原始字串中的位置」。 我們可以透過深度優先搜尋 (DFS) 從後綴樹轉換成後綴陣列,也可以使用 SA-IS algorithm 1 直接在 O(n) 時間內產生後綴陣列。 有了後綴陣列,就可以透過 binary search 在 O(mlogn) 內完成搜尋。
以 reference ABCAB read BC 為例,後綴陣列 [5,3,0,4,1,2] 搜尋過程如下:
0: ABCAB$ 5: $ 5: $ < B
1: BCAB$ 3: AB$ 3: A < B
2: CAB$ sort 0: ABCAB$ search 0: A < B
3: AB$ ======> 4: B$ =========> 4: B = B => $ < B
4: B$ O(n) 1: BCAB$ O(mlogn) 1: B = B => C (index=1)
5: $ 2: CAB$ 2: C > B
後綴陣列的資料結構比後綴樹簡單很多,只需要 O(n) 空間即可,適合拿來處理非常大的文本資料。 此外,還可以用其他技術(如 Burrows-Wheeler Transform 和 FM-index)進一步壓縮並加快搜索。
Burrows-Wheeler Alignment
在生物資訊學領域,目前主流使用 Burrows-Wheeler Transform (BWT) 和 FM-index 來做基因比對,常見的工具有 BWA、Bowtie。 BWT 與 suffix array 很像,但是採用循環字串,也就是將後綴不足的長度補齊,且同樣經過排序的過程。 轉換後的矩陣最後一行 (column) 即是 BWT 的輸出,即 BWT(AGCAG$) = GC$AAG。
0: AGCAG$ 5: $AGCAG
1: GCAG$A 3: AG$AGC
2: CAG$AG sort 0: AGCAG$
3: AG$AGC ======> 4: G$AGCA
4: G$AGCA O(n) 1: GCAG$A
5: $AGCAG 2: CAG$AG
經過排序後,BWT 的輸出容易讓相同的字連在一起,常見的應用是 run-length compression (eg. bzip)。 例如 GC$AAG 可以壓縮成 GC$2AG,如果是 AGCAGCAGC$ 經過 BWT 就可以壓縮成 3C$3A3G。 那為什麼不要直接排序並壓縮原始字串呢?因為這樣就無法還原了。 所以 BWT 是一種無損壓縮的技術,對於像基因這種重複性很高(只有 A、T、C、G)的大數據非常有用。 2
在討論如何利用 BWT 做字串搜尋前,我們先來定義某個字元的 rank 為「這個字元在這個位置前出現過的次數」,並將 rank 用下標註記。 例如上述字串可以標記為 A0G0C0A1G1$ ,如果我們經過 BWT 轉換會產生以下陣列:
$ A0 G0 C0 A1 G1
A1 G1 $ A0 G0 C0
A0 G0 C0 A1 G1 $
G1 $ A0 G0 C0 A1
G0 C0 A1 G1 $ A0
C0 A1 G1 $ A0 G0
如果我們特別關注第一行 (F) 與最後一行 (L),可以觀察到一個很重要的現象:任意字母在 F 與在 L 出現的順序是一致的,例如字母 G 在 F 與 L 的 rank 順序都是 [1, 0]。 換句話說,在 F 與在 L 的第一個 G 在原字串是同一個字元。 這其實也不難理解,因為字串本身是循環建立,而陣列又經過排序, 這代表我們可以從字母在 L 的關係中推估出在 F 的關係,反之亦然。 這即是 LF Mapping。
實際上我們在比對字母時,會於不同列 (row) 之間不斷縮減範圍,所以 rank 會由上往下建立。 例如共有 10 個 A、20 個 G、30 個C,我們想查看 C10 開頭的列, 就要去看 row 1$ + 10A + 20G + 10C = row 41。
5 0: $ A1 G1 C0 A0 G0
3 1: A0 G0 $ A1 G1 C0
0 2: A1 G1 C0 A0 G0 $
4 3: G0 $ A1 G1 C0 A0
1 4: G1 C0 A0 G0 $ A1
2 5: C0 A0 G0 $ A1 G1
有了 BWT 與 LF Mapping 的知識,我們就可以開始搜尋了。 例如我們的目標 read 為 AG,我們會從最後一個字倒著比對回去。 對於字母 G,我們可以搜尋所有 G 開頭的列,得到 row index 3-4。 下一個目標是 A,我們從 row 3-4 的尾端搜尋 A 的 rank 範圍,得到 A 0-1。 接著回到開頭,搜尋 A 0-1 為 row 1-2。 最後我們比對 suffix array,得到 row 1-2 的值是 [3,0]。 這兩個位置即是 AG 在 AGCAG 的位置。
Read: A'G' Read: 'A'G SA
0: $ .... G 0: $ .... G 5: $
1: A .... C 1: "A .... C" "3: AG$"
2: A .... $ find A(0-1) O(n) 2: "A .... $" check SA "0: AGCAG$"
3: "G .... A" ====================> 3: G .... A ==========> 4: G$
4: "G .... A" check row(1-2) O(1) 4: G .... A O(1) 1: GCAG$
5: C .... G 5: C .... G 2: CAG$
同理,如果我們要比對的字串不存在(例如 GA)。 首先我們在第一行找到 A 開頭的範圍 row 1-2,接著觀察尾端會發現只有 C、$,代表目標不在 reference 內。 我們可以使用以下程式碼來實作 BWT 比對,注意這裡使用 recursion 來方便理解過程,若 read 過長則建議使用 iteration 來避免 call stack。
# Python3
def BWA(band_start: int, band_end: int, read: str, index: int) -> int:
if index == -1:
return band_start, band_end # find read
if band_start == band_end:
return -1, -1 # no match
s = read[index]
rank_start = Rank(s, band_start)
rank_end = Rank(s, band_end)
return BWA(bands[s]+rank_start, bands[s]+rank_end, read, index-1)
我們可以發現,雖然每次做 LF mapping 都會不斷縮減範圍,如果只是逐項查找 L 上目標字元的 rank(即上面程式碼 Rank() 的實作方式),仍會需要花費 O(n) 的時間複雜度。 另外,雖然 BWT string 可以被無損壓縮,suffix array 或 rank 依然需要花費 O(n) 的空間來儲存,對於大數據來說不夠友善。 為了解決這個問題,目前的 BWT 演算法都會額外建立 FM-index 來作為快速比對的依據。 3
FM-index 分為三個部分:第一部分是最重要的 F 與 L。 L 是 reference 的 BWT string,所以會與原始文本長度相同 O(n),但可以被壓縮。 F 理論上可以透過排序 L 來產生,但為了節省處理時間,通常會額外建立字典記錄每個字母的開頭位置(即上面程式碼的 bands[]),所以是 O(1)。 至於 BWT 矩陣中間的其他項( F ~ L 中間灰色的部分),通通不重要,所以不用紀錄。
第二部分是每個字元在 L 的 rank。以前面為例,當我們搜尋 AG 並找開頭到 G 的位置在 row 3-4 時,需要有某種方法快速找到尾端 A 的範圍。 一個有效的方法是建立每個字元數量的 prefix sum array,就可以在 O(1) 時間內查表。 例如從下表可以查到 row 3-4 的 A 數量在 1-2 的區間,代表接著要找開頭第 1-2 個 A (rank 0-1)。
L | A G C
G | 0 1 0 <== checkpoint 1
C | 0 1 1
$ | 0 1 1
A | 1 1 1 // A = 2 in row5 - 1 A in row4,5 = 1
A | 2 1 1 // A = 2 in row5 - 0 A in row5 = 2
G | 2 2 1 <== checkpoint 2
以長度 n 的基因序列 (ATCG) 為例,就會需要 4n 空間來建立這個 prefix sum array。 我們可以每 k 列建立一個 checkpoint,只記錄其內容,剩下都省略。 這樣當需要查表的 index 落在 checkpoint 以外時,就可以根據附近的 checkpoint 與 L 來回推該處的真實數字。 這個作法看似很複雜,但因為 k = constant,所以依然可以控制時間複雜度為 O(1),並大幅縮減空間複雜度為 O(n/k)。
第三部分是 suffix array。當我們找到 L 中的 A 範圍後,就可以透過 suffix array 回推其在 reference 的座標。 與前面 prefix sum 類似,我們不要儲存整個 suffix array,而是每 k' 列儲存一次 checkpoint。 接著我們就可以透過 LF mapping 的方式,一路前後比對計算該位置的實際值。 例如我們要找 A 在 SA' 的值,經過幾次比對(循環字串的位移)即可搜到 checkpoint,相加後可得真實數字。 這個作法一樣可以確保我們在 O(1) 時間內查表,並將空間控制在 O(n/k')。
F L SA'
$ G 5 <== checkpoint 1
A C 3 // A0 (F) map to C0 (L) in row5, SA = 2 + 1 (map one times) = 3
A $ 0 // A1 (F) map to $0 (L) in row0, SA = 5 + 1 (map one times) = 6//6 = 0
G A 4
G A 1
C G 2 <== checkpoint 2
至此我們針對 BWT 演算法做個總結:
在時間方面,建立 FM-index (包含 LF 與 prefix sum、suffix array 的 checkpoint)需要花費 O(n) 時間, 搜尋字串(包含 prefix sum 與 suffix array 特定位置的計算)需要花費 O(m) 時間。
在空間方面,以人類基因體為例(長度約 3*109),假設每個鹼基用 2bit 來儲存,k = 1/128、k' = 1/32。 F 需要 2*4 = 16 bytes,L 需要 2bits * 3G = 750 MB,PS = 4bytes * 4 * 3G / 128 ~= 400MB,SA = 4bytes * 3G / 32 ~= 400 MB, 總會需要 1.5GB 的空間。對比 suffix tree 約需要 45GB、suffix array 約需要 12 GB,可說是非常優秀。
如果上面文字太過冗長,可以參考網路上這份 投影片,以圖文方式講解得非常清楚。
Fuzzy Search
截至目前為止,我們已經快速帶過幾個常見的字串搜尋演算法,並將搜尋的時間複雜度提升到 O(m)。 但仍有一個待解決的重要議題,那就是「模糊搜尋」。
在生物資訊學研究中,我們偶爾會發現基因在複製過程中產生了突變,造成 reference 序列與 read 序列並不相等。 如果今天我們只想觀察整體現象,大可將這些少量突變忽略不計;但有時候這些突變正是我們想研究的關鍵資訊,不可能視而不見。 例如我先前曾參與有關 Crosslink Induced Mutation Sites (CIMS) 的研究, 大抵就是透過突變(尤其是 deletion)資訊來回推可能的蛋白質殘留物,進一步推測 sRNA 與 mRNA 的結合位置。 甚至我們先前曾有一篇發表在 Science 的研究 4,就是以統計的角度,提出 piRNA 在各區域中對於 mismatch 容忍度的結合公式。
要分析 mismatch 的發生,我們可以直接延用前文的 BWT 演算法,要點是將 BWT 陣列切分成數個字母區域,再依序計算每個區域剩餘可用的 mismatch 數量。 例如 reference 為 AGCAG read 為 AC,預計容忍 mismatch 的數量為 1。 首先比對末端 C,我們可以先依據第一行的字母將 BWT 陣列拆分為剩餘 mismatch = 0 (A、G) 與 1 (C); 進接著進入下一層比對 A,得到 row1-2 的位置 AG (M=1) 與 row4 的位置 GC(M=1),剩下都是 M = 2。
5 0: $AGCAG
3 1: AG$AGC 0
0 2: AGCAG$
4 3: G$AGCA 0
1 4: GCAG$A
2 5: CAG$AG 1
我們可以使用下列程式碼來實作含 mismatch 的比對:
# Python3
def BWA(band_start, band_end, mismatch_left, read, index):
if index == 0:
return band_start, band_end
if band_start == band_end:
return None
ans = []
next_character = read[index-1]
for s in "ATCG":
rank_start = Rank(s, band_start)
rank_end = Rank(s, band_end)
if s == next_character: # exact match
ans += BWA(bands[s] + rank_start,
bands[s] + rank_end,
mismatch_left, read, index-1)
elif mismatch_left > 0: # mismatch
ans += BWA(bands[s] + rank_start,
bands[s] + rank_end,
mismatch_left-1, read, index-1)
return ans
然而,儘管 BWT 可以拿來分析 mismatch,卻不能直接分析 INDEL (insertion or deletion)。 這也是為什麼 Bowtie (2009) 只支援 mismatch, 到了 Bowtie2 (2012) 才開始支援 INDEL。
一般來說,我們可以透過動態規劃 (dynamic programming) 來計算兩個字串間的編輯距離 Edit Distance (Levenshtein Distance)。 編輯距離常見於自然語言模型 (NLP model) 在計算文本之間的誤差程度,並以此作為反向傳播的依據。 詳細作法可以參考 LeetCode 72. Edit Distance。
另一種我覺得很有趣的方式是 Bitap 演算法, 儘管搜尋本身的時間複雜度不是非常優秀,但因為使用 bitwise operation,所以在 INDEL 不多的前提下依然很快。 首先建立 read 對不同字母的 bitmask,再將狀態逐步 left-shit 並對 bitmask(ref) 做 OR。 如果要做模糊搜尋也很容易,設定各種情境並將結果 AND 起來即可。 詳細運作流程可以參考下圖(GenASM 的論文 5),其中 D = deletion、S = subsitution (mismatch)、I = insertion、M = match。
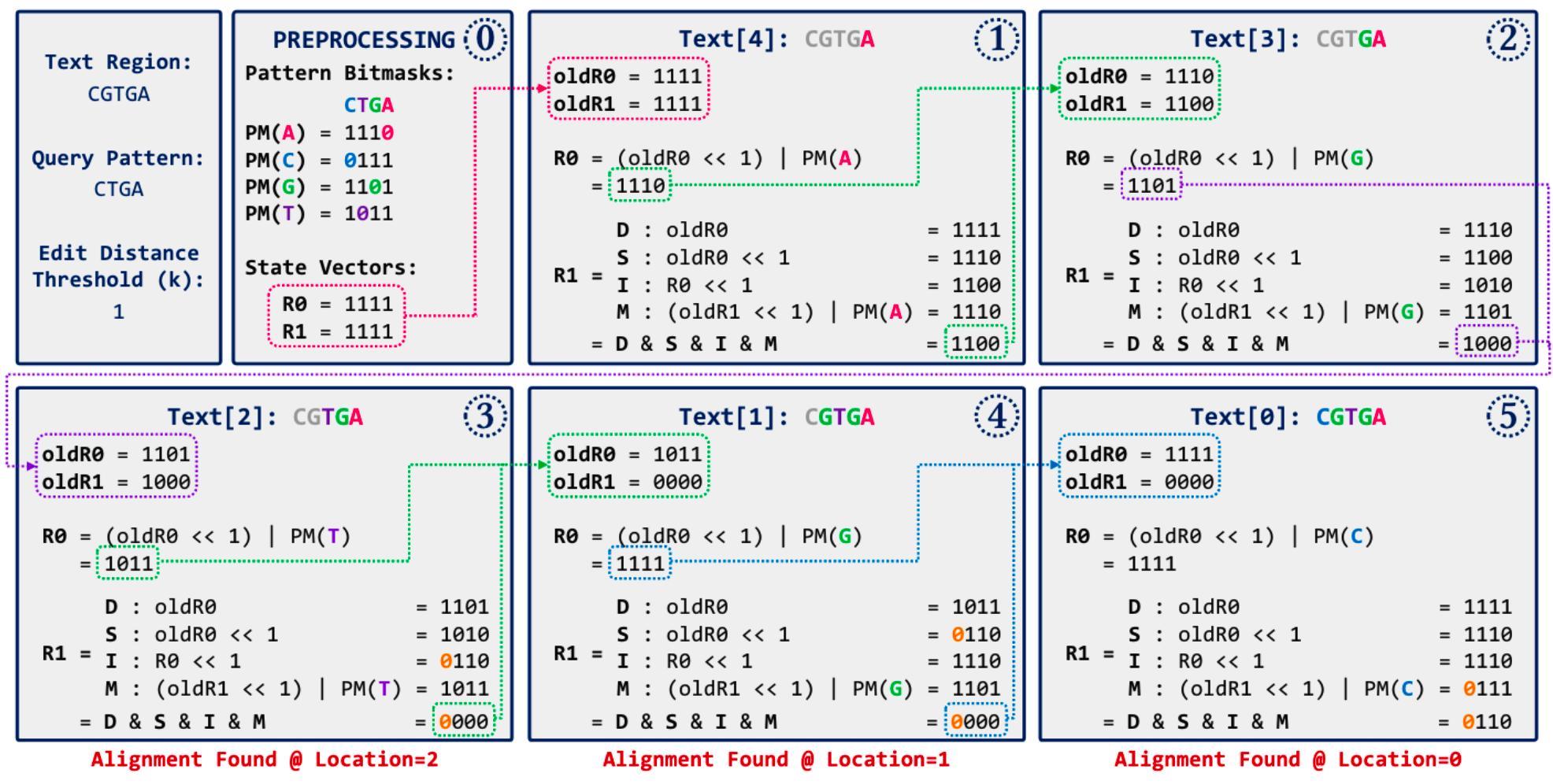
實際上為了加速運算,很多基因比對工具都會混合上述的幾種方式。 例如將 read 拆分成幾個短片段,稱為 seed。 實際比對時,會透過 BWT + FM-index 優先尋找 seed perfect match (or mismatch = 1) 的段落, 再往兩旁做 extension,以動態規劃或 bitap 的方式拓展 INDEL 的搜尋範圍。
照這個邏輯,豈不是 seed region 內要幾乎完全正確才能讓整條 read 被比對到嗎? 這正是這種演算法的主要困難之處。 透過調整 seed 長度、彼此之間的距離、mismatch 數量、甚至是 re-seed 的次數,可以增加 read 被比對到的機率,卻有可能大幅降低比對的效率。 Bowtie2 稱之為 trade-off between speed and accuracy,並設定幾個參數作為調整方式。 例如 seed 間距預設是一個以 read 長度為變數的方程式 ,當長度越長時,就透過更長的間距(更稀疏的 seed)增加搜尋的效率。
在基因比對中,面對數以百萬計的 read 與龐大的基因體,以及眾多 mismatch 所造成的相似答案, 我們不再追求什麼是真正「正確」的位置,而是設定不同情境所造成的 penalty。 例如 mismatch 扣 2 分、deletion 或 insertion 扣 5 分等,再藉由 score threshold 來過濾所有可能的答案。 將答案整理成表格後,我們習慣以 CIGAR string 記錄 INDEL 的位置,並將結果儲存成 SAM/BAM 或 CRAM 格式。
至此字串搜尋不再只是一個單純的比對問題,而是在不斷優化時間與空間消耗的前提下,統計並觀察大數據所呈現的趨勢。 除了上文所提及的演算法,還有許多新的技術不斷被發表,例如 HISAT2 使用 graph-based alignment,號稱比 linear-genome (eg. BWA) 更快更省空間 。 而這正是生物資訊學在做的其中一件事,用 computer science 的方式輔助研究,拓展數據分析的可能性。
Footnotes
Nong, Ge, Sen Zhang, Wai Hong Chan, "Linear suffix array construction by almost pure induced-sorting." data compression conference, IEEE, 2009. ↩
Burrows M, Wheeler DJ, "A block sorting lossless data compression algorithm", Digital Equipment Corporation, Palo Alto, CA 1994, Technical Report 124; 1994 ↩
Paolo Ferragina, Giovanni Manzini, "Opportunistic data structures with applications." Foundations of Computer Science, 41st Annual Symposium, IEEE, 2000. ↩
Zhang D, Tu S, Stubna M, Wu WS, Huang WC, Weng Z, Lee HC, "The piRNA targeting rules and the resistance to piRNA silencing in endogenous genes", Science. 359, 587-592, 2018 ↩
Cali, Damla Senol, et al. "GenASM: A high-performance, low-power approximate string matching acceleration framework for genome sequence analysis." 53rd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), IEEE, 2020 ↩