- Published on
Resonant Circuits for Wireless Power Transfer
- Authors

- Name
- Ryan Chung

一、前言
本專題主要在探討近場傳輸中,透過諧振磁耦合電路來達成無線傳能的方法。 儘管無線傳能的設計已有諸多文獻可以參考,卻較少有從原理開始從頭分析,乃至設計線圈阻抗與幾何形狀的論文。 故本次專題即是建立在諸多研究上,期望透過整合不同人設計線圈的方式,配合理論與實務,完成近場磁耦合之無線高效傳能線圈的設計。
二、原理分析與系統設計
2.1 原理分析
諧振磁耦合 (magnetic resonant coupling) 是用於無線傳能 (wireless power transfer, or WPT) 中很常見的技術, 它透過一組或多組的線圈來傳遞能量,並藉由調變其 RLC 阻抗來達成阻抗匹配,使得兩邊的諧振頻率 (resonant frequency) 相同,以提高其能量傳輸效率 (power transfer efficiency, or PTE)。 其簡易螺線管模型如下圖 1-a,power source 將能量傳入主線圈 (primary coil, L1),並透過磁場耦合至次線圈 (secondary coil, L2),最後送至負載端。 其能量傳輸的距離與效率取決至耦合係數 (coupling coefficient, k)。 一般來說,兩線圈之互感 (mutual inductance, M) 可經由 Biot-Savart Law 推導為以下關係式:
其中, 為真空中的磁導率 (permeability), 為兩線圈之匝數。 我們可以進一步將互感與耦合係數改寫成以下關係式:
藉由上述公式,便可以簡易推導耦合係數與線圈的距離、形狀等幾何關係。
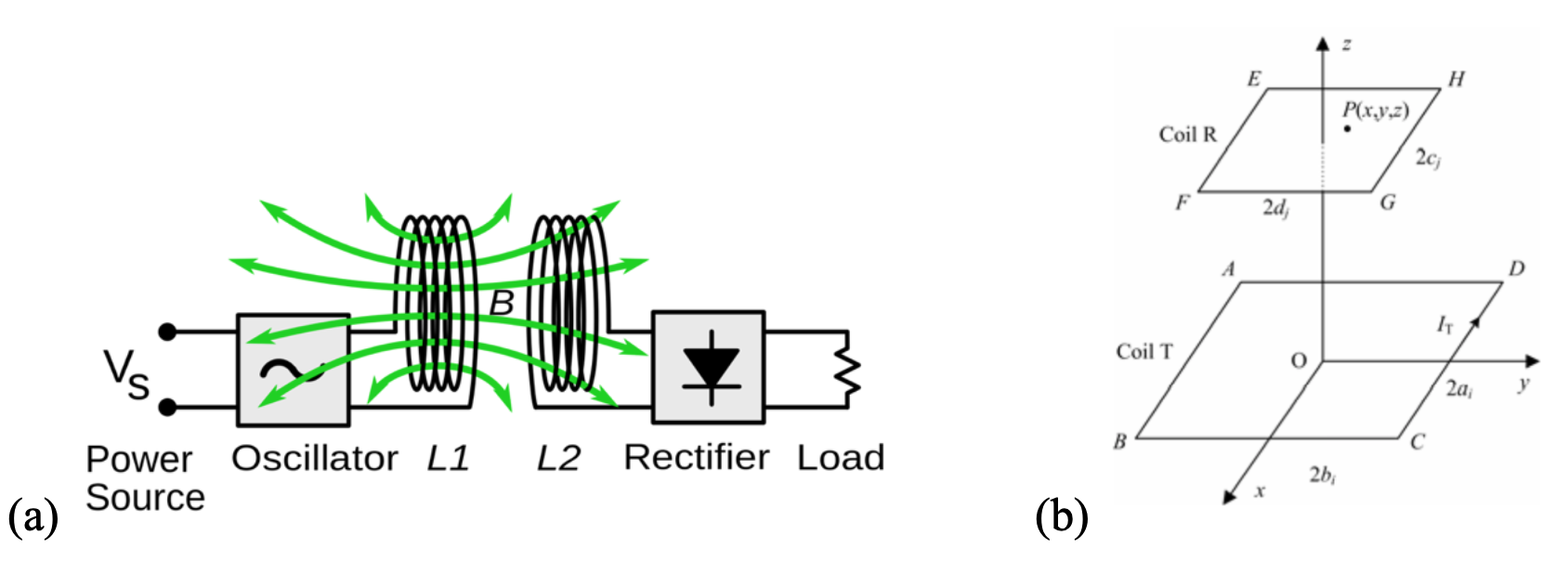
Fig. 1. (a) Simply block diagram of a two-coil resonant WPT system.
(b) Two coaxial single-turn filament rectangular coils' configuration.
若耦合線圈為矩形 (如上圖 1-b),可以透過優先推導單邊導線對線圈所產生的磁通,再將四邊導線相加,即可獲得單位電流下的互感值。 其中單邊導線 CD 所產生之互感可推導為以下之關係式:
除了上述之二線圈諧振電路,更常用的模型為四線圈電路,如下圖二。 透過一對 Transmitting (TX) coil 與 Receiving (RX) coil 來傳遞磁場能量。
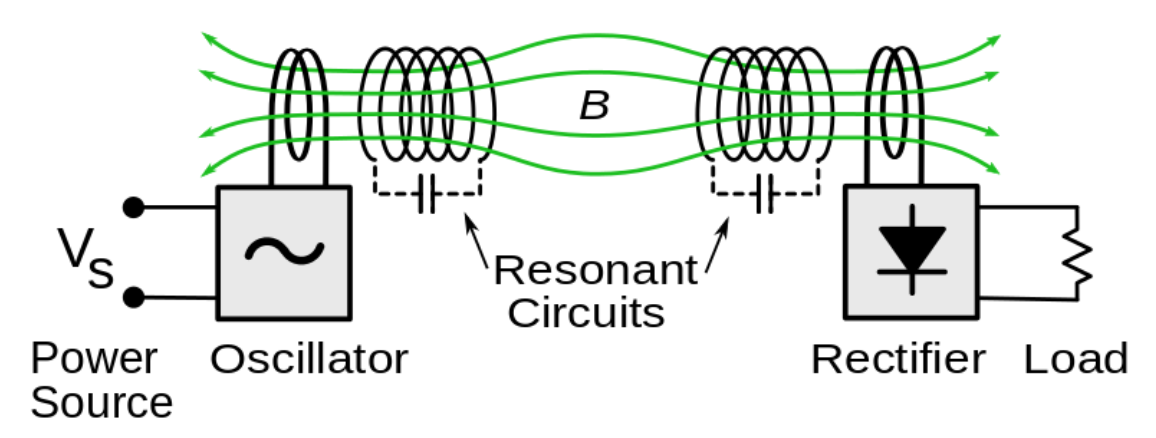 Fig. 2. Simply block diagram of a four-coil resonant WPT system.
Fig. 2. Simply block diagram of a four-coil resonant WPT system.其等效電路如下圖三(a)。在線圈彼此距離夠大的情況下,遠端的互感相對較小,其耦合係數可以省略 (相關比較可參閱 1)。 在諧振頻率下,其等效電路整合如下圖三(b),其中,因為阻抗匹配 (),透過 KVL 可推導得:
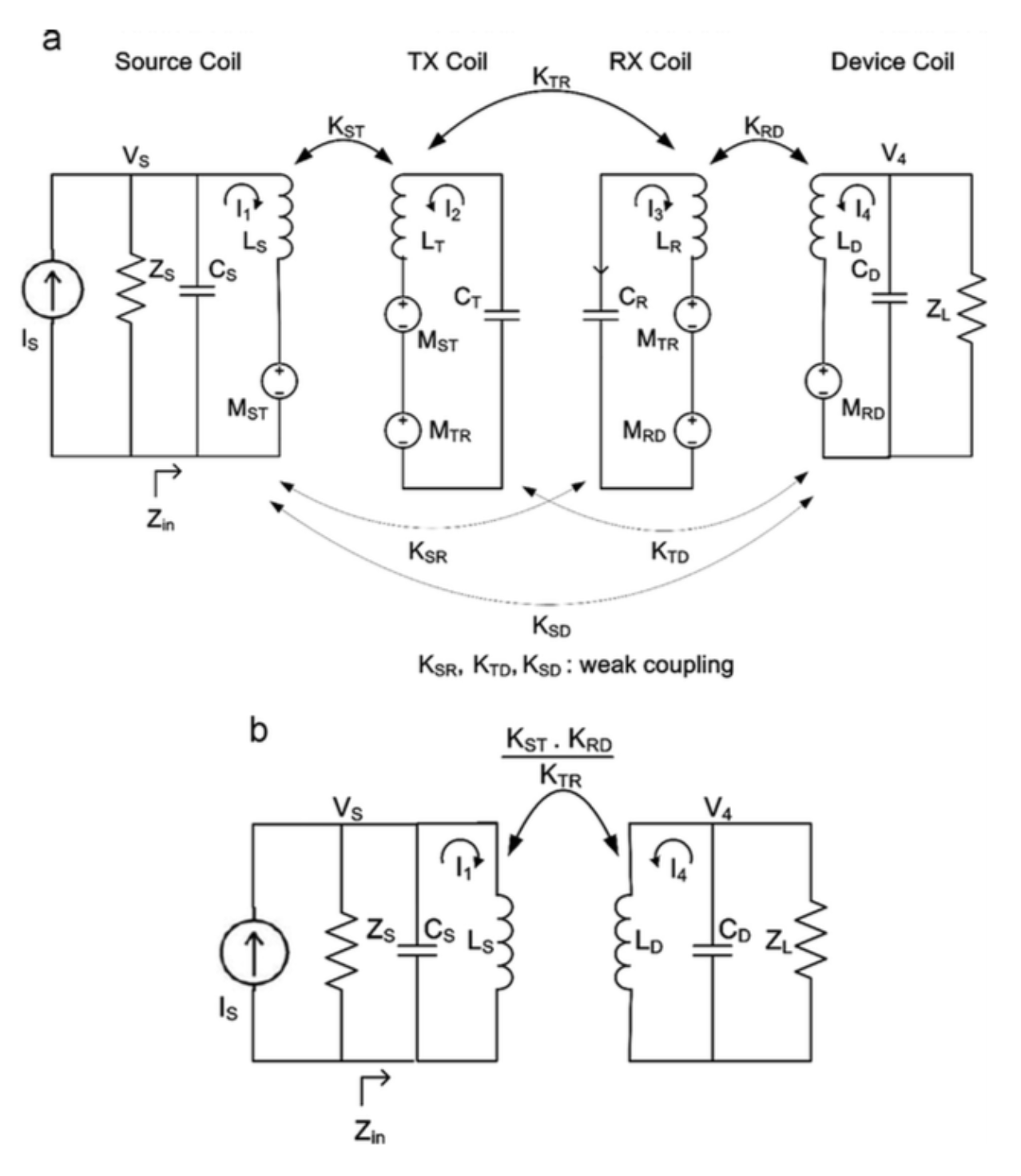
Fig. 3. (a) Equivalent circuit model of a 4-coil resonant WPT system.
(b) Simplified circuit at the resonant frequency.
由以上公式搭配前文,即可以設計出四線圈諧振電路的模型。 然而必須注意的是,諧振電路存在頻率分裂 (frequency splitting) 的現象,當相圈彼此距離夠近時,諧振頻率會逐漸分裂並拉遠成高低頻兩半,如下圖四。 若我們透過 S 參數表達其傳輸效率 (S21) 對頻率的關係,可以明顯看出隨著距離拉近,位在諧振頻率中間的效率顯著地下降,若要改善其現象,除了動態調變 RLC 值之外,就只能設計好傳輸頻率,以防止效率下滑過於嚴重。
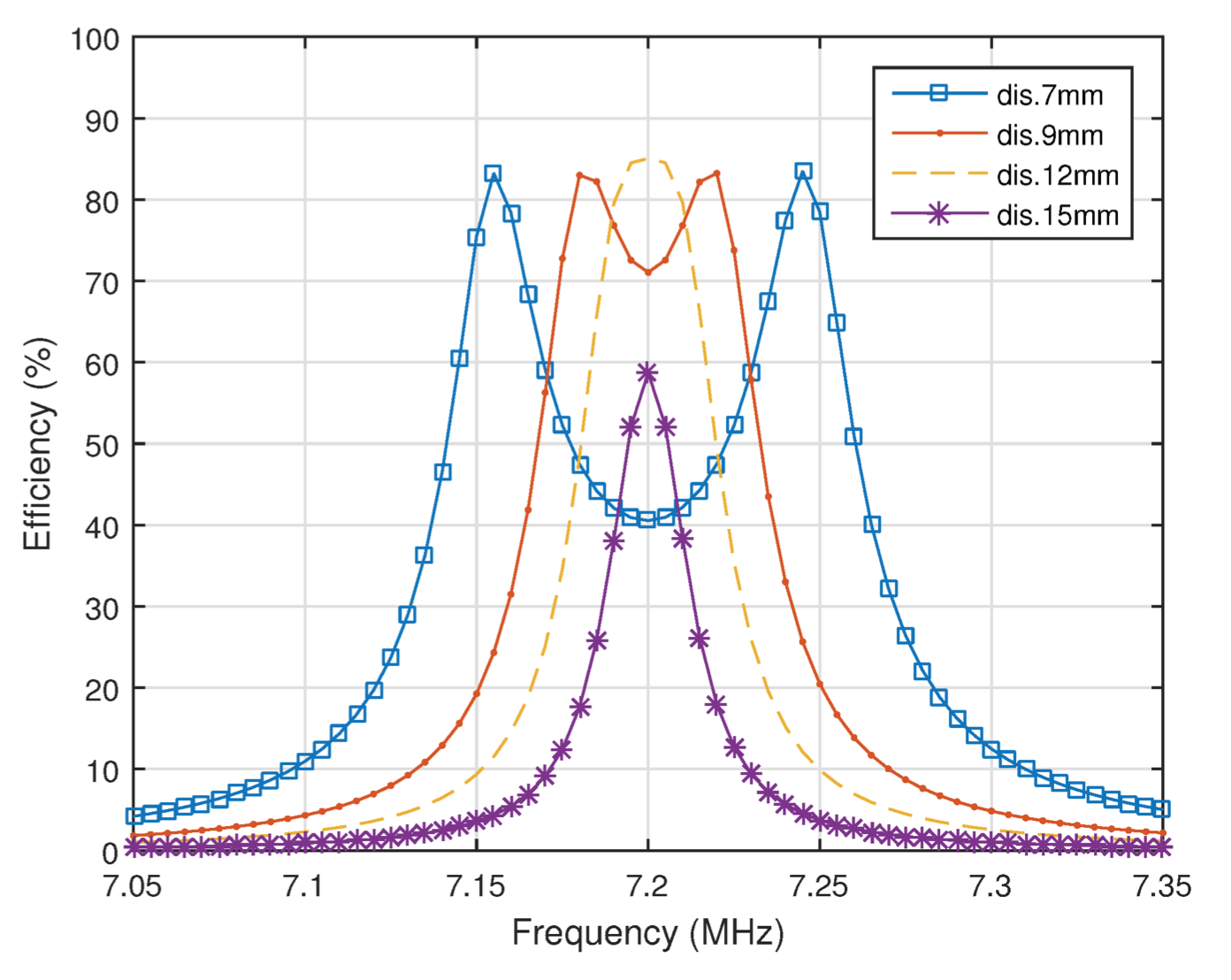 Fig. 4. Frequency splitting phenomenon in different distances.
Fig. 4. Frequency splitting phenomenon in different distances.2.2 系統設計
以上幾個重點即為 WPT 之諧振電路的設計基礎。 在本次專題中,除了理論分析外,也利用 ANSYS 公司出的 High Frequency Structure Simulator (HFSS) 軟體來進行線圈模擬(如下圖五)。 透過觀察其反射係數 (S11)、傳輸效率 (S21)、磁場分佈與諧振頻率之間的關係來設計電路,此流程不僅能夠實際模擬電路的磁場行為,對於功率轉換的結果也能有更清楚的認識。
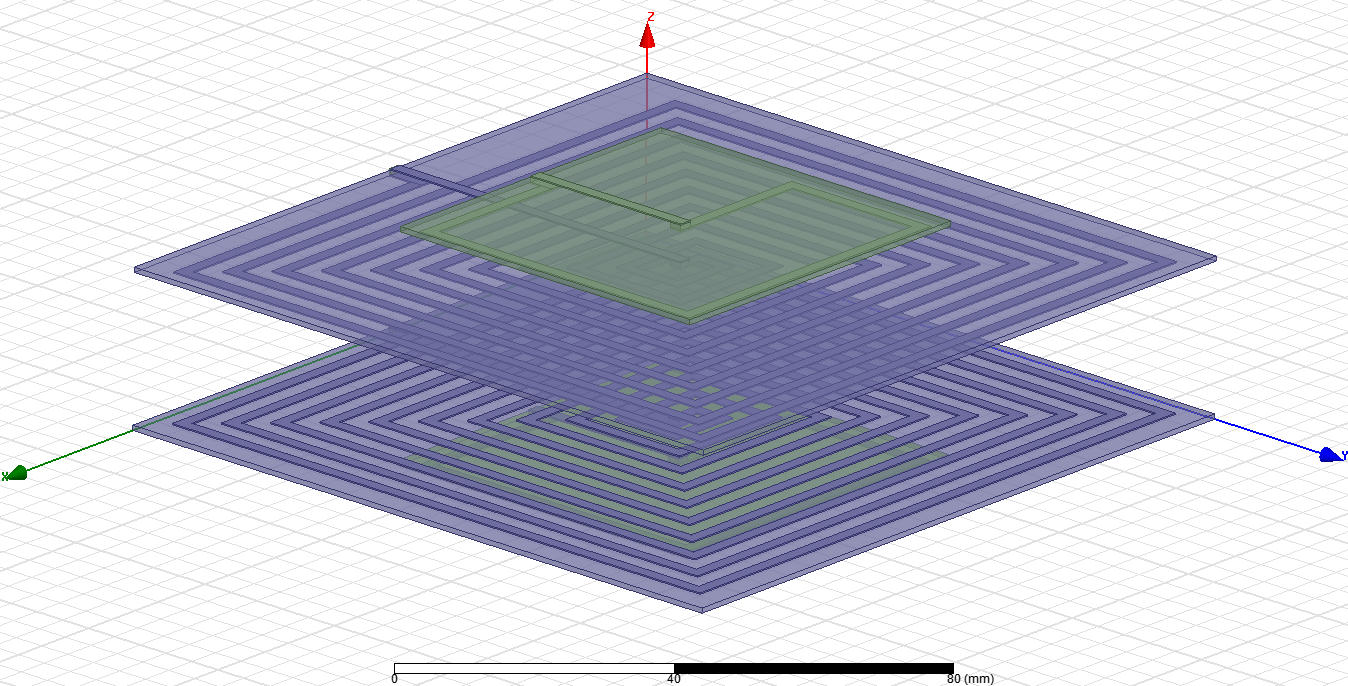 Fig. 5. Four-coil resonant module in HFSS.
Fig. 5. Four-coil resonant module in HFSS.如下圖六、七即為四線圈模型在 distance=10mm 下於 HFSS 的模擬情形。
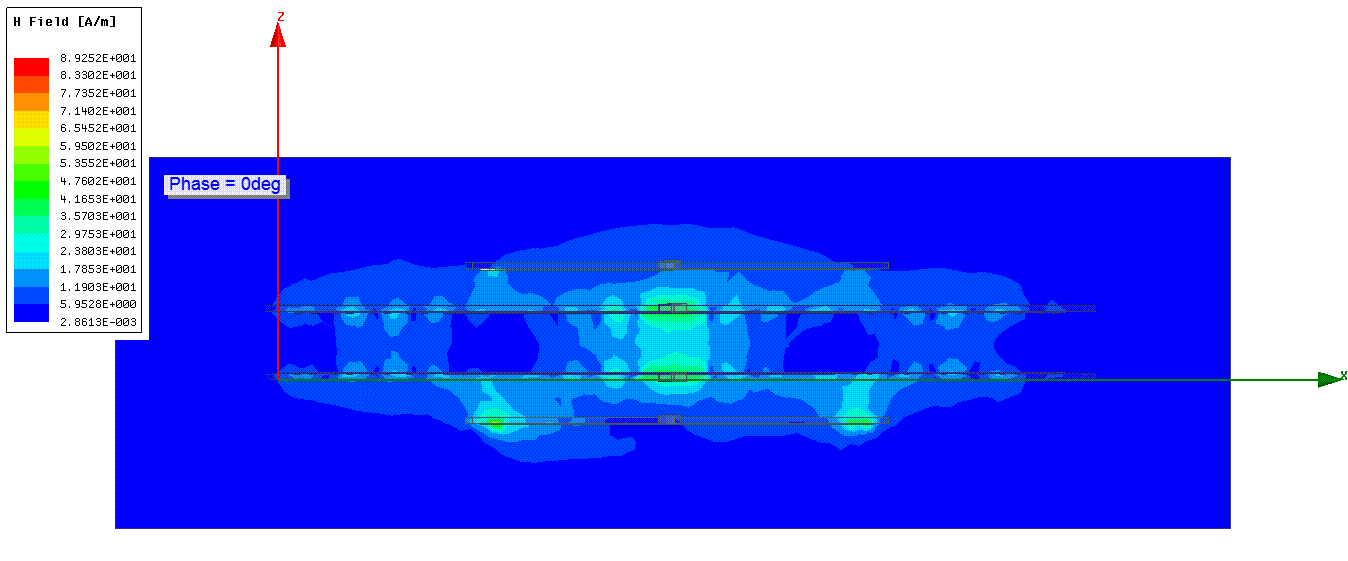 Fig. 6. H field of four-coil resonant module in HFSS.
Fig. 6. H field of four-coil resonant module in HFSS.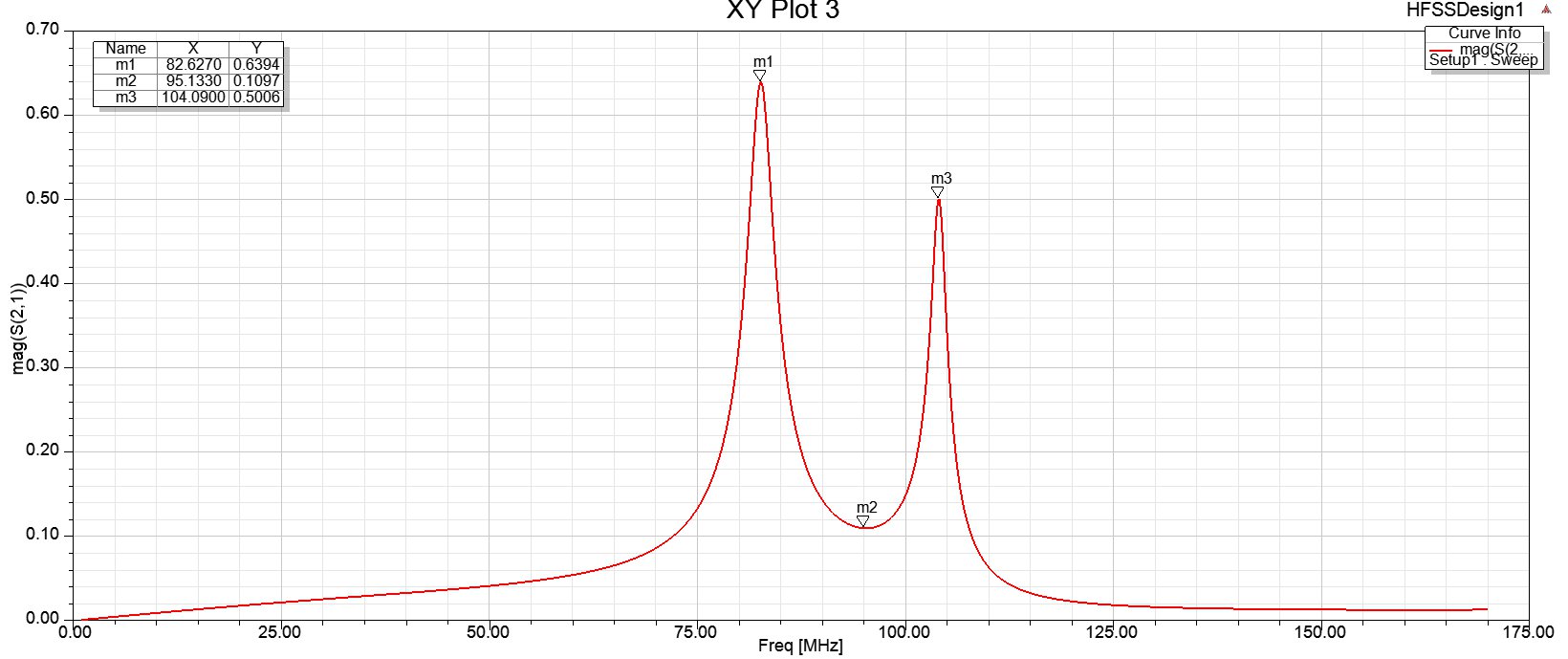 Fig. 7. S21 of four-coil resonant module in HFSS with frequency splitting.
Fig. 7. S21 of four-coil resonant module in HFSS with frequency splitting.三、實驗結果
為了符合實際應用,本次實作預計將諧震頻率設計在 13.56MHz,即近距離無線通訊 (Near-field communication, or NFC) 的頻率,為了減少幾何形狀與寄生電容所產生的誤差,將匝數限制在單圈。 其線圈相關參數可參考下表一。
| 規格 | 參數 | 規格 | 參數 |
|---|---|---|---|
| 諧震頻率 | 13.56 MHz | 等效電感 | 0.27 μH |
| 串聯電容 | 0.5 nF | 寄生電阻 | 7 mΩ |
| 導線直徑 | 1 mm | 線圈長寬 | 10*6 cm |
透過 Matlab 模擬以上電路,可以繪出基於不同頻率、距離所產生之 S21 值,如下圖 8-a 所示。 若將能量傳遞效率與傳輸功率對線圈距離作圖,可以繪出其關係如下圖 8-b 所示。 由兩張圖我們可以清楚發現,當線圈距離在 4 公分時,功率傳輸產生極大值,若將線圈繼續靠攏,則會產生頻率分裂現象,傳輸功率進而下降。
(a) 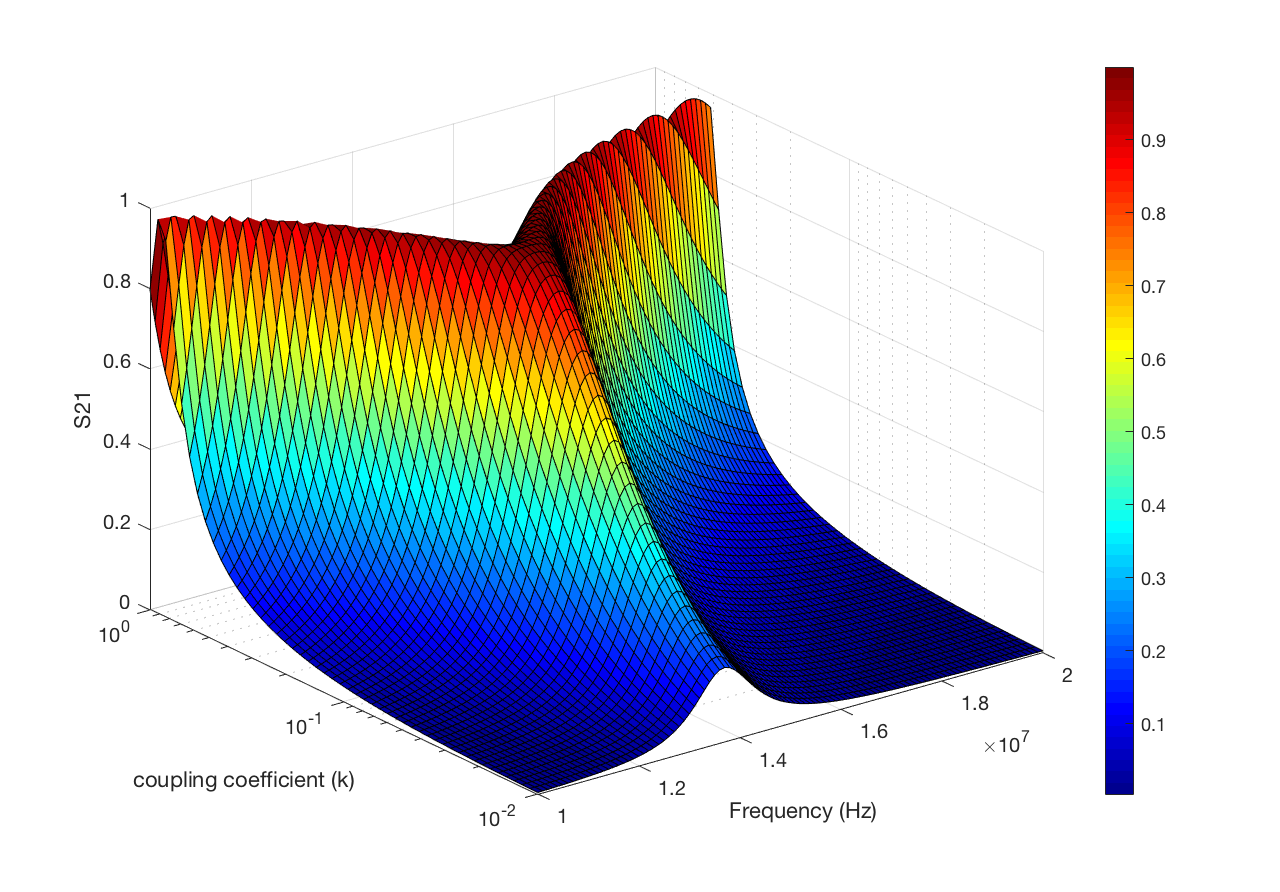 (b)
(b) 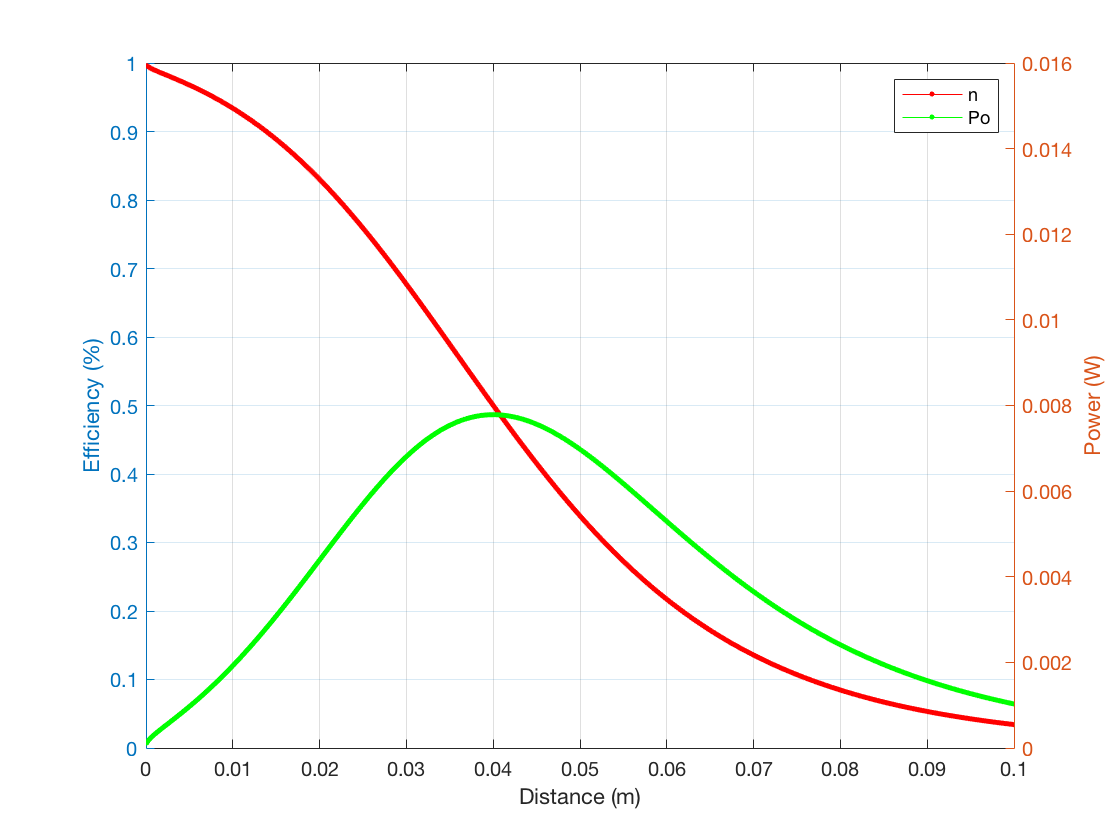
Fig. 8. (a) The frequency splitting phenomenon in different distances.
(b) Power efficiency and transferred in different distances.
其實際電路如下圖九所示,透過一根直徑 1 mm 的銅線,我們可以做出兩個長寬為 10 cm 和 6 cm 的矩形線圈,符合一般手機充電模組之大小。 其測量結果如下圖十,由圖中可以清楚看見當頻率在 12 MHz 附近時,產生明顯的功率傳輸現象。
(a)  (b)
(b) 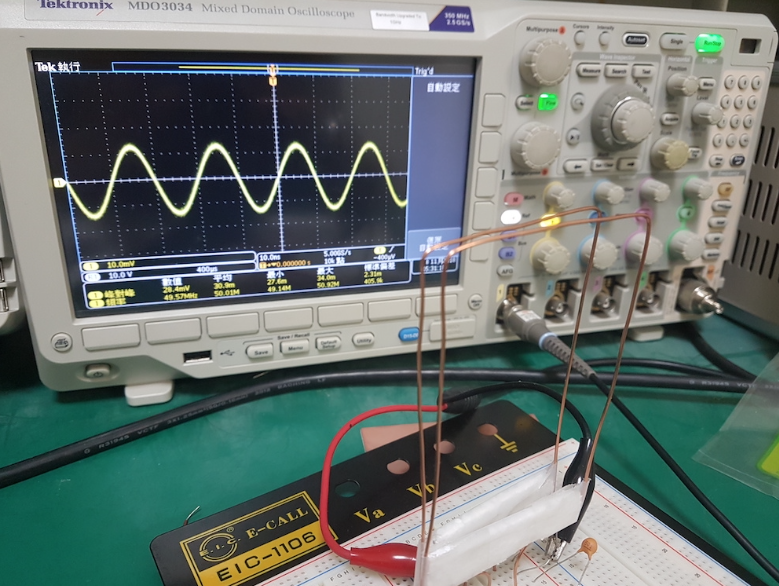
Fig. 9. (a)(b) Implementation of wireless power transfer circuit.
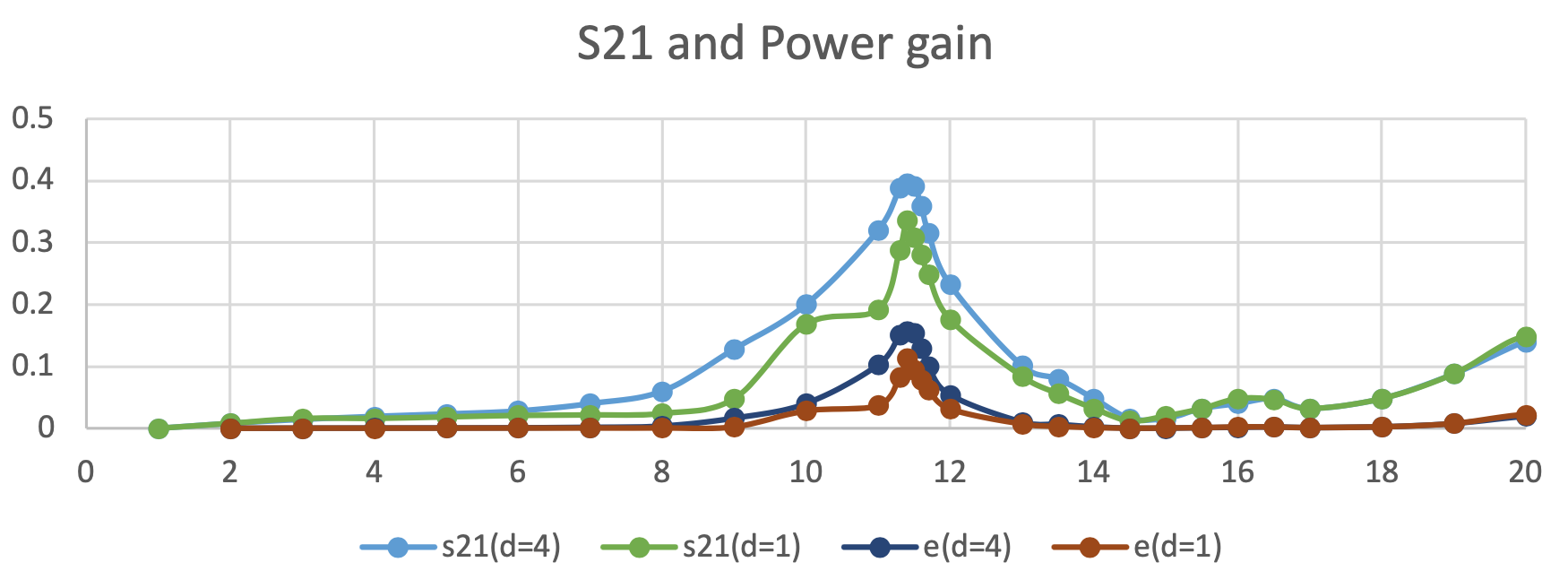 Fig. 10. The actual performance in different frequencies and distances.
Fig. 10. The actual performance in different frequencies and distances.四、結論
這次的專題主旨在透過研究無線傳能電路的原理和參數,包含不同幾何形狀的互感、最大功率轉移、頻率分裂等現象,設計出適合的模型並實際做出成品。 儘管因為等效電感、寄生電阻等問題,造成實際諧振頻率略有偏移,大方向的電路設計依然是成功的,唯效能問題尚無法完全改善,這有待更進一步的分析與檢討,才能調整出最適合的電路參數。
五、參考文獻
Footnotes
Y. Zhang, Frequency-Splitting Analysis of Four-Coil Resonant Wireless Power Transfer. IEEE Antennas and Wireless Propagation Letters, Vol. 13, 2014. ↩ ↩2
R. Huang, Frequency Splitting Phenomena of Magnetic Resonant Coupling Wireless Power Transfer. IEEE, Vol. 50, No. 11, 2014. ↩
SD. Barman, Wireless powering by magnetic resonant coupling: Recent trends in wireless power transfer system and its applications. pp. 1525-1552, 2015. ↩
DW. Seo, Study on Two-Coil and Four-Coil Wireless Power Transfer Systems Using Z-Parameter Approach. ETRI Journal, Vol. 38, No. 3, 2016. ↩
K. Fotopoulou, Wireless Power Transfer in Loosely Coupled Links: Coil Misalignment Model. IEEE Transactions on Magnetics, Vol. 47, No. 2, 2011. ↩
AP. Sample, Analysis, Experimental Results, and Range Adaptation of Magnetically Coupled Resonators for Wireless Power Transfer. IEEE Transactions on Industrial Electronics, Vol. 58, 2011. ↩
ML. Kung, Dual-band coil module design for near-field WPT systems. 2017 ↩
Y. Cheng, A New Analytical Calculation of the Mutual Inductance of the Coaxial Spiral Rectangular Coils, 2014. ↩
H. Zhou, Modelling and Practical Implementation of 2-Coil Wireless Power Transfer Systems, 2014. ↩