Buck Converter for Energy Harvesting

一、前言

隨著光獵能系統的興起，為了有效的降低其輸出電壓，設計一個高效能的 DC-DC converter 便成為一個重要的議題。 然而傳統的線性電源 (linear regulator) 因效率不彰，需要龐大的散熱器來散熱，造成許多空間與能源的損耗。 與之相對，開關電源 (switching converter) 具備損耗小、發熱低、體積小、重量輕的特性，在使用上更為靈活。 實際上，線性電源與開關電源往往搭配著使用，利用線性電源獲取精度要求較高的電壓輸出，並利用開關電源獲取精度要求較低、能量耗損較少的輸出。

本次專題即是以光獵能系統中的降壓型電源轉換器 (buck converter) 為主，分析其設計原理和電路架構，並進一步進行實作和測量。

二、原理分析與系統設計

2.1 原理分析

Switching converter 的構造如圖 1-1 ¹，可以簡化為一組直流輸入、一組直流輸出，以及一組訊號控制單元。 利用此訊號控制單元來切換內部的開關，將直流輸入的電壓在 V_S 與 0 之間切換，以此方式降低此電路在時域上的電荷數，並利用一組 LC 低通濾波電路 (low-pass filter) 來進行穩壓，最後達到所要求的電壓輸出。 另外，在 closed-loop 的概念中，則是會額外加上一組迴授電路，用以檢驗其輸出是否達成標準，再進一步調整其 PWM 控制訊號。

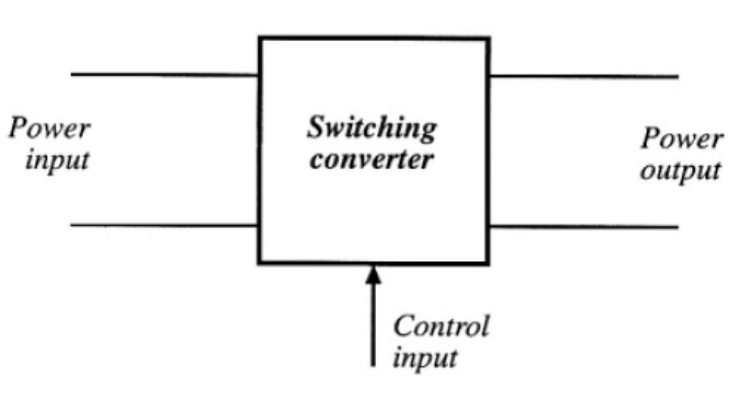圖 1-1 switching converter 簡圖

圖 1-2 為常見的幾種 DC-DC switching converter ²。 根據不同的應用功能，可分為 buck converter、boost converter，或是混和型 buck-boost converter，以及改良型 Cuk converter。 利用訊號的輸入與 L、C 的搭配來達成各種電源轉換的目的。

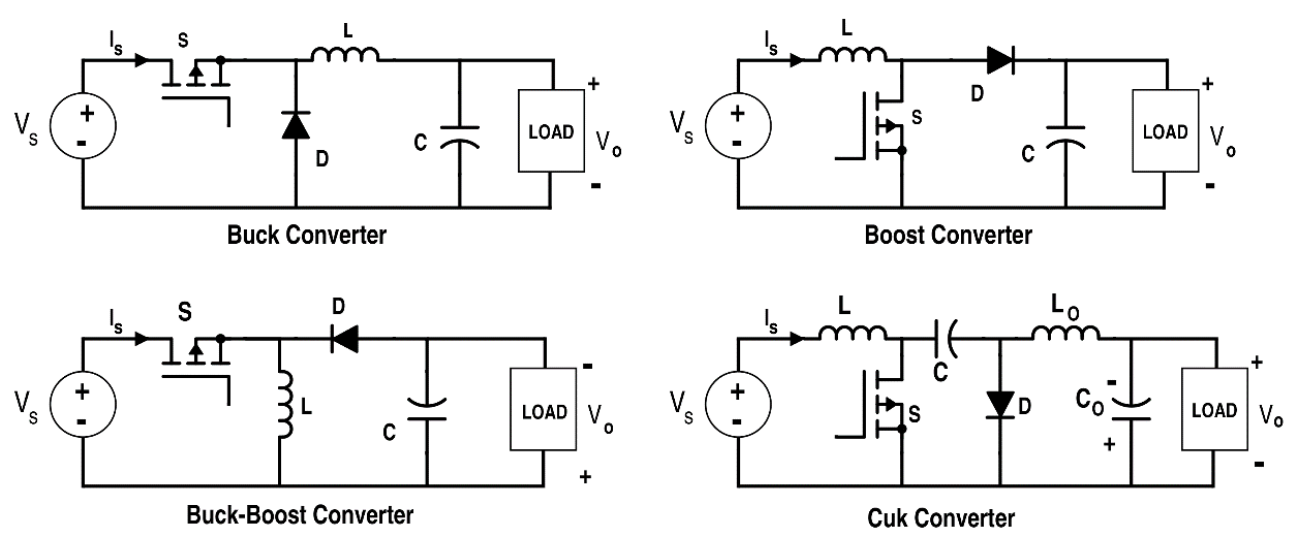圖 1-2 常見的幾種 DC-DC switching converter

本次光獵能電壓轉換器的重點 buck converter 之 open-loop 電路圖如圖 1-3 ³，其構造分別為一端直流輸入 VS，一顆訊號開關 power MOSFET (S)，一顆飛輪二極體 (D)、一組電感 (L) 和電容 (C)，以及一端負載 (R)，並對應到輸出電壓 V_O。 power MOSFET 和 diode 扮演著 switch 的角色，透過 gate 極輸入 PWM 訊號來製造電流切換，也可以透過雙 switches 來取代 freewheeling diode，減少功率消耗以增加其效能 (相關討論在第二節)。 L 與 C 則扮演著儲能與濾波的功能，當 switch 接通時儲存能量，switch 斷開時提供能量，讓整個電路可以保持流通，同時降低其 V_O 的 ripple。

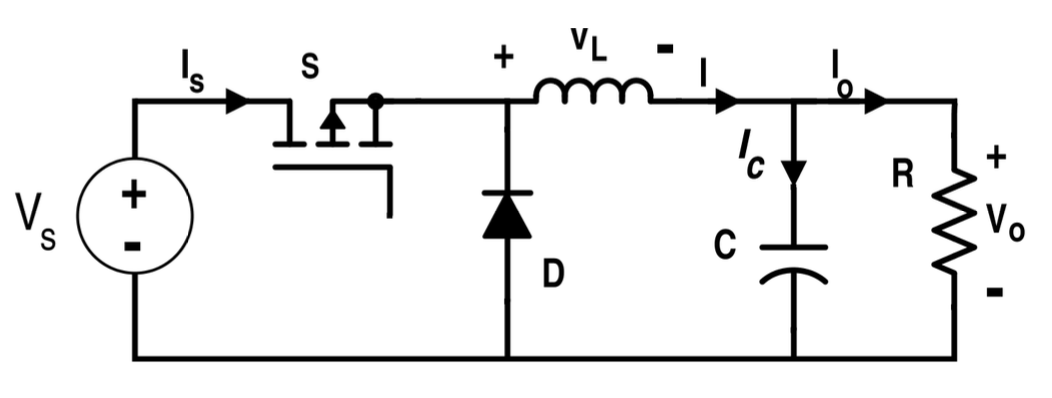圖 1-3 open-loop 狀態下 buck converter 的電路簡圖

若我們將接上 switch 後的電壓源對 PWM 週期作時域分析，可以得到圖 1-4 的關係圖 ⁴。 其中，TS 為週期，switch 切換通路的時間比則稱為 duty cycle (D)。 由圖可知，藉由 switch 的切換，可以將電路分為兩種 state (如圖 1-5 所示) ⁵。 一種是開關通路時 (On-State)，電壓源直接接上 L、C，為儲能元件充能；另一種是開關開路時 (Off-State)，由儲能元件供給整個電路能量，以維持輸出電壓的穩定。

值得注意到的是，由於 duty cycle 的不同，造成電感電流有放盡的可能，這使得此類電源轉換器分成 continuous conduction mode (CCM) 與 discontinuous conduction mode (DCM) 兩種模式。 本篇主要探討 CCM 的模式下 buck converter 的種種元件特性。

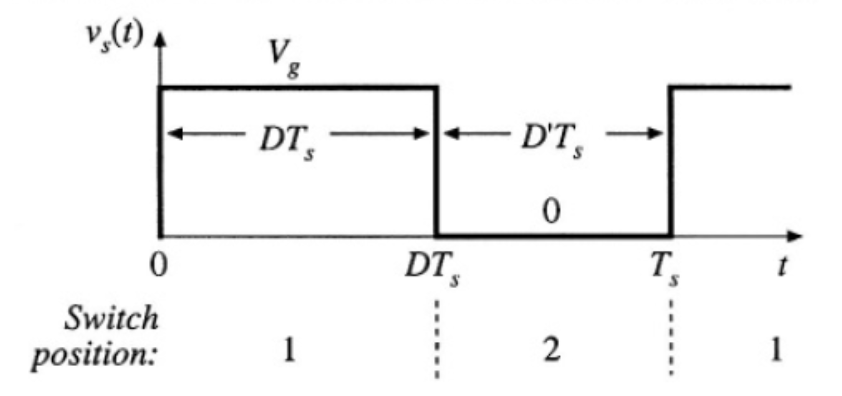圖 1-4 switch 對電壓源造成 VS 與 0 間的升降

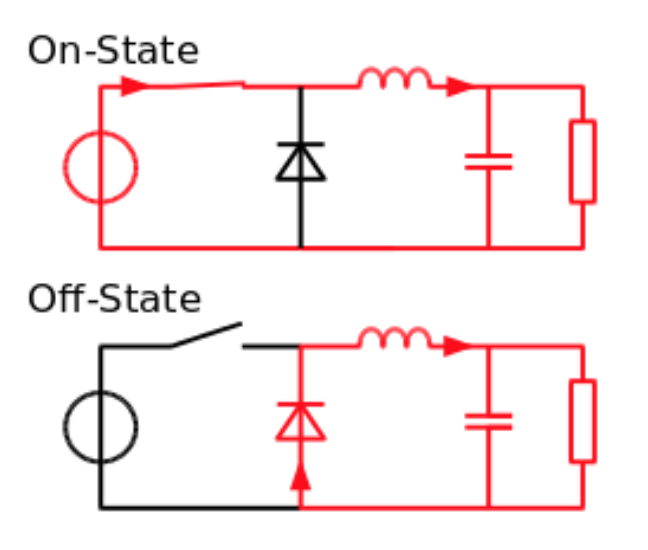圖 1-5 兩種狀態下的 buck converter 電路簡圖

在分析電路前，首先必須注意一件事情。一個正常的開關電路必定存在不理想的諧波 (harmonics)，使得輸出電壓不完全呈水平，為一直流輸出加上微小漣波 (ripple)，如圖 1-6 ⁶。

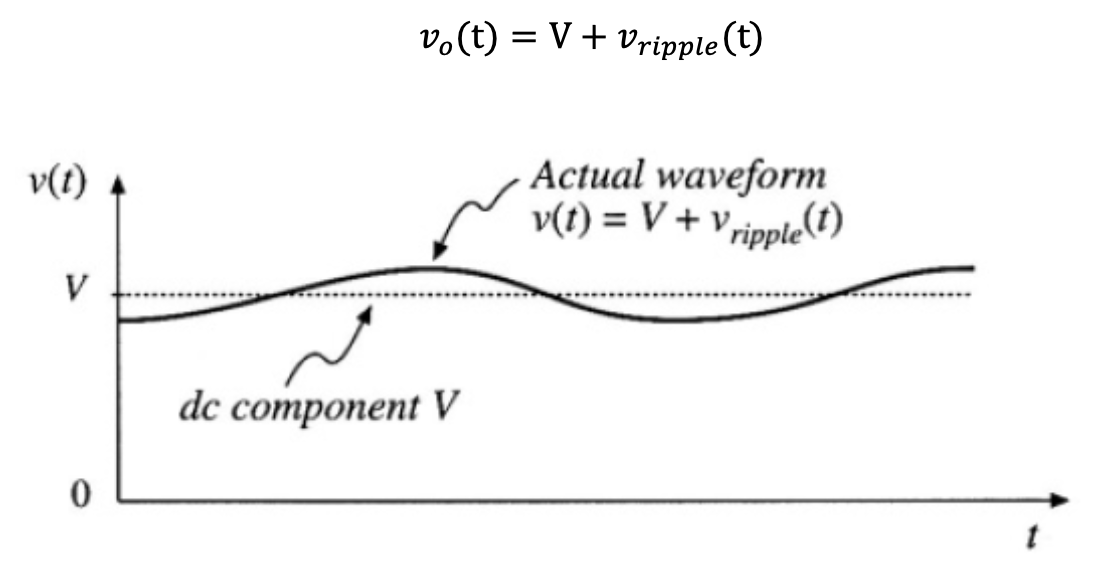圖 1-6 Real output voltage waveform.

然而，一個設計良好的濾波電路勢必將 ripple 的影響降到極小，使得 $|v_{ripple}|$ 的值遠小於平均電壓值 V。 根據 small ripple approximation，$v_o(t)$ 將會約略等於 V。關於 $v_{ripple}$ 的數值將會在後面的段落進行實際推算。

回頭分析電壓輸入端，當電路處於 On-State，根據 Kirchhoff's voltage law (KVL)，$V_S = V_L + V_O = L\dfrac{di}{dt} + V_O$ ； 當電路處於 Off-State，$V_O = -V_L = -L\dfrac{di}{dt}$ 。 又因為 $V_O$ 等於定值 V，所以 $L\dfrac{di}{dt}$ 便為定值，使得電感電流 $i_L$ 的斜率為定值。 整理合併兩種 state 後，可以繪出 $i_L$ 對時間的關係圖在穩態時如圖 1-7 ⁷。

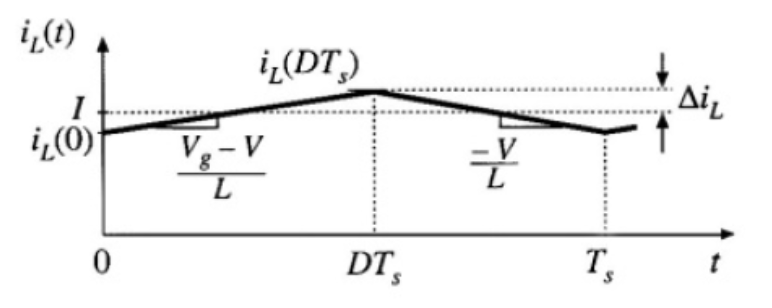圖 1-7 Steady-state inductor current waveform.

與此同時，其電感電壓為 $V_S - V_O$ ，可以對時間繪出如圖 1-8 的關係 ⁸。

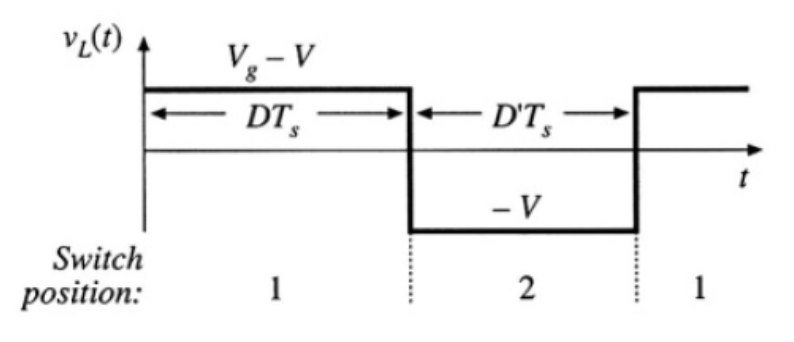圖 1-8 Steady-state inductor voltage waveform.

分析以上兩張圖可以表示出其電流變化的關係式:

$\Delta I_{(ON)} = I_{Max} - I_{min} = \dfrac{1}{L} \int_{0}^{DT} V_L\:dt = \dfrac{ V_S - V_O }{L}\:DT$

$\Delta I_{(OFF)} = I_{min} - I_{Max} = \dfrac{1}{L} \int_{DT}^{T} V_L\:dt = \dfrac{ - V_O }{L}\:(1-D)\:T$

在穩態時，$\Delta I_{(ON)} + \Delta I_{(OFF)} = 0$，其代表電感電流的升降及電感電壓的上下面積必須相等。 整理以上方程式可得結論公式： $V_O = D V_S$。 這代表在理想的狀況下，buck converter 的電壓輸出完全取決於電壓輸入和 duty cycle。

另外，從以上電流關係式也可以整理出其平均電流變化量：

$| \Delta I_L | = \dfrac{ V_S - V_O }{2L} DT = \dfrac{ V_O }{2L}\:(1-D)\:T$

接著分析輸出端。在穩態時，因為電容的電荷充放必須守恆，所以其電壓升降會相等。 由公式 $V_C(T) - V_C(0) = \dfrac{1}{C} \int_{0}^{T} I_C\:dt = 0$ 可以看出，其電流對時間的積分為 0，代表其線下面積總和為 0，電流的平均值 $< I_C > = 0$ ，如圖 1-9 所示 ⁹。

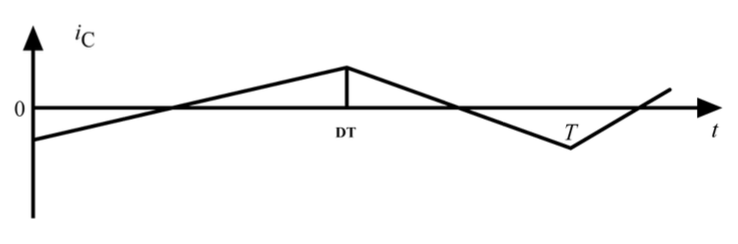圖 1-9 Steady-state capacitor current waveform.

根據 Kirchhoff's current law (KCL)，電感電流 $I_L = I_O + I_C = \dfrac{Vo}{R}$ 。 所以，電感電流的平均值 $<I_L> = \dfrac{I_{Max}+I_{min}}{2} = \dfrac{V_O}{R}$ 。

整理以上公式，即可求出電感電流的最大和最小值：

$I_{Max} = DV_S\:(\dfrac{1}{R}+\dfrac{1-D}{2L}\:T)$

$I_{min} = DV_S\:(\dfrac{1}{R}-\dfrac{1-D}{2L}\:T)$

最後，由 $I_C$ 圖形下面積求得 $\Delta Q = \dfrac{1}{2} \dfrac{I_{Max}-I_{min}}{2} \dfrac{T}{2}$，我們可以進一步計算輸出電壓的 ripple 值： $\Delta V_O = V_{ripple} = \dfrac{\Delta Q}{C} = \dfrac{D(1-D)}{8LC}\:V_S\:T^2$。 如前文所述，在理想的狀態下，此數值必定遠小於輸出電壓 $V_O$。如果將 $I_L$ 與 $I_C$ 對時間的關係圖相比較後，對齊整理如下圖 1-10 ¹⁰，可見電容的作用為濾除電感電流的 ripple。

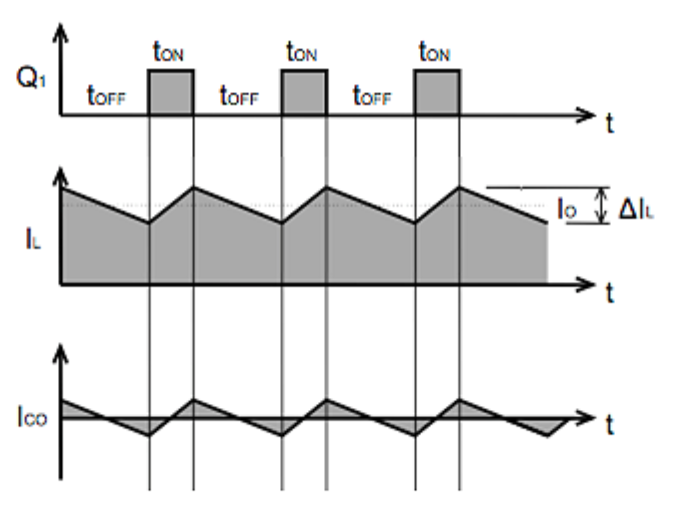圖 1-10 Current waveform of each part.

2.2 系統設計

於實際系統加上非理想 ESR、ESL 後，整理目前的 buck converter 電路和 其元件波型如下圖 2-1 所示，其中紅色為電壓波型，綠色為電流波型 ¹¹。

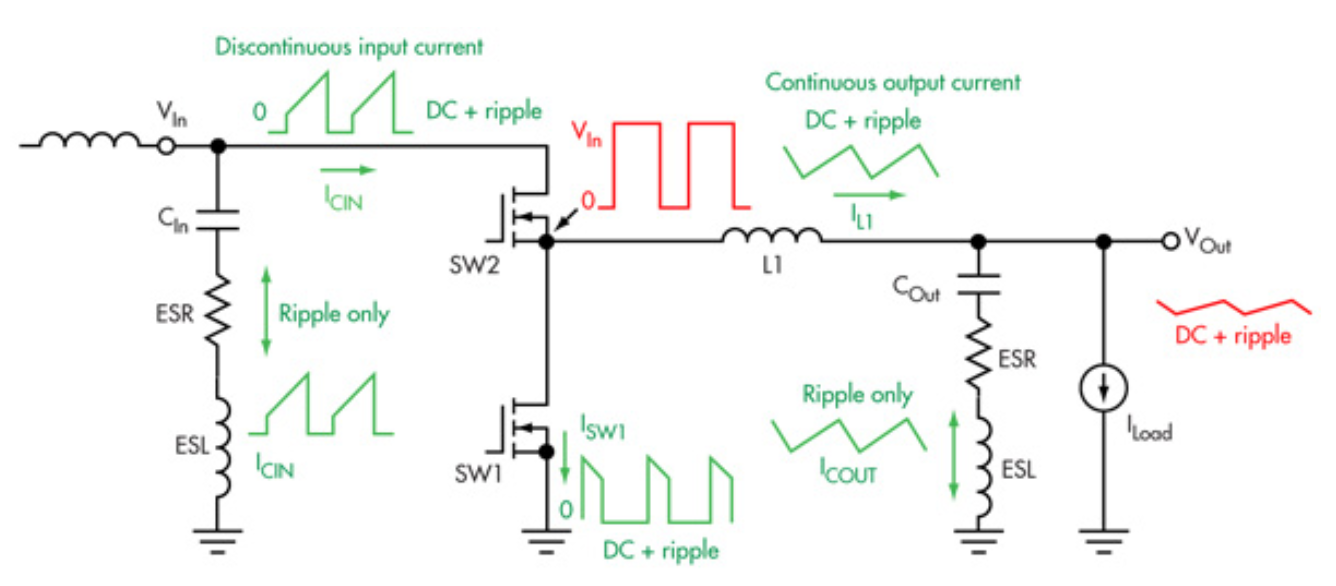圖 2-1 A buck converter design with waveform.

首先討論 buck converter 中 duty cycle 的設計。考慮到開關和二極體所消耗的電壓，其輸出與輸入的關係式須改寫為：

$(V_S - V_{MOS} - V_O)\:T_{ON} = (V_O + V_{Diode})\:T_{OFF}$

一旦其輸出電壓 $V_O$ 確定，就可以從其最小的直流輸入 $V_{S,min}$ 找出其相對應的最大 duty cycle ($D_{Max}$)，進而重新整理公式：

$D_{Max} = \dfrac{V_O + V_{Diode}}{V_{S,min} + V_O + V_{Diode}} \approx \dfrac{V_O}{V_{S,min}}$

接下來討論電感 (L) 的設計。當開關閉合時 ($T_{ON}$)，電感將能量儲存在磁場中；當開關打開時 ($T_{OFF}$)，電感將能量釋放回電路中，並提供直流輸出的基礎電壓，同時與電容 (C) 組成一個 LC 低通濾波器。 我們若要讓 buck converter 保持在 CCM 的模式下，勢必確保其電感電流大於 0，所以其電流變化必須控制在一個範圍之內。在此我們定義其輸出電流的變化量為平均值的 k 倍:

$\Delta I_L = k\:I_{L,avg} = \dfrac{V_S-V_O}{2L}\:DT = \dfrac{V_O}{2L}\:(1-D)\:T$

整理其電感的關係式為以下方程式：

$L = \dfrac{(V_S-V_O)\:D}{2k\:F_{PWM}\:I_{L,avg}} = \dfrac{V_O\:(1-D)}{2k\:F_{PWM}\:I_{L,avg}}$

由以上方程式可以看出，電感 L 與訊號頻率 $F_{PWM}$ 成反比。 若要維持電流在特定範圍內，增加 $F_{PWM}$ 即可減少電感的大小。 然而，增加 $F_{PWM}$ 其實會增加開關的能量耗損，所以 $F_{PWM}$ 通常介於 100~500kHz 之間 ¹²。 另外，在 Fun-damentals of Power Electronics 一書中則將其範圍界定在 1k~1MHz 之間 ¹³。

再來討論電容 (C) 的設計。因為經由電感出來的電流往往帶有很大的起伏，造成輸出電壓不穩定的 ripple，所以選用適當的電容可以降低其 ripple 的大小。 由前文的公式可以看出，電容值與 ripple 值成反比：

$C_O = \dfrac{\Delta Q}{\Delta V_O} = \dfrac{D(1-D)}{8L\:\Delta V_O}\:V_S\:T^2$

另外，考慮到非理想寄生電阻 (ESR) 的存在，輸出電壓的 ripple 必定會受其 ESR 所影響。 若定義輸出電壓的最大承受 ripple 為 $\Delta V_{O,Max}$，則 $\Delta V_C$ 和 $\Delta V_{C,ESR}$ 的總和必然會小於等於 $\Delta V_{O,Max}$。 整理其相關公式得以下結論：

$C_O = \dfrac{\Delta I_L\:D}{F_{PWM}\:(\Delta V_{O,Max}-R_{ESR}\:\Delta I_L)}$

接下來分析 MOSFET 和 Diode 的設計。在預期中，MOSFET 必須要能接近理想的開關，具備極低的電阻和極高的切換效率。 如下圖 2-2 所示，MOSFET 在通路 ($T_{ON}$) 時壓差接近 0，其電流等同於輸入電流 $I_L$ ;在開路 ($T_{OFF}$) 時承受最大壓差 ($V_S$)，同時其電流接近 0。 Freewheeling diode 與其相反，在通路 ($T_{ON}$) 時須要承受最大壓差 $-V_S$ ，在開路 ($T_{OFF}$) 時則有最大電流 $I_L$ ¹⁴。

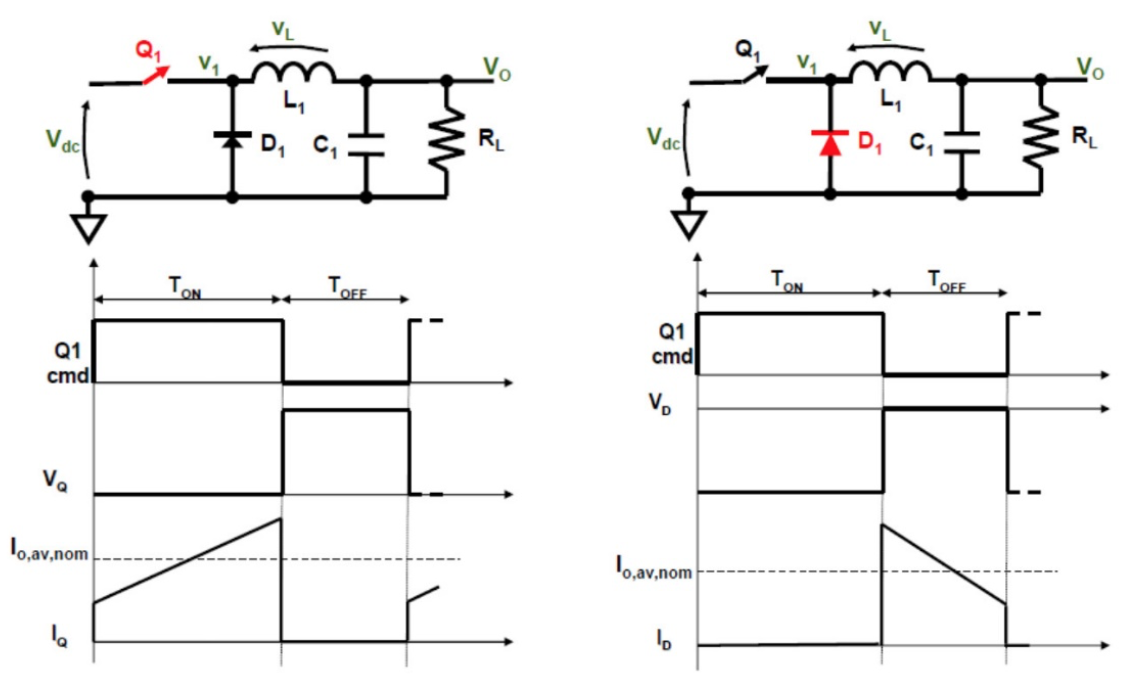圖 2-2 Switch and Diode waveform.

整理 MOSFET 的電壓、電流值公式為以下兩項：

$V_{Q,Max} = V_{S,Max} + V_{D,on}\; ; \;I_{Q,avg} = I_{L,avg}\:D$

整理 Diode 的電壓、電流值公式為以下兩項：

$V_{D,Max} = -V_{S,Max} + V_{D,on}\; ; \;I_{D,avg} = I_{L,avg}\:(1-D)$

為了降低功率損失，有些 converter 會將二極體替換成電晶體，改成雙 Switch 的設計 (Synchronous rectification)。 考慮二極體導通時的功率耗損 $P_D = V_D\:(1-D)\:I_L$，若以開關 $S_2$ 代替，其功率耗損 $P_{S2} = I^2_L\:R_{DSON}\:(1-D)$。 在 $R_{DSON}$ 非常低的情況下，對應到 duty 相對較小的時候，能產生較大的功益。 然而，雙開關意味著更高的成本，且為了避免 shoot through，必須設計將彼此的開關時間稍微延遲，使其增加了電路複雜度和少量的能源消耗。

最後來簡單討論 Closed loop 的電路設計。 在原先 open loop 的設計中，為了達成變壓的目的，透過固定的 PWM 訊號來達成預期的 duty。 然而在實際情況下，可能因為諸多因素 (例如：輸入電壓改變、元件特性、溫度升降、噪訊等等)，造成輸出電壓的不穩定。 為了改善這種狀況，closed loop 在電路中增加了一組或多組的檢測電路，透過迴授系統傳達給訊號產生器，再進一步調整新的頻率來符合預期的輸出。

下圖 2-3 為 closed loop 的基本設計概念 ¹⁵。 透過一個 Sensor gain 將輸出電壓拉出，與參考電壓 (Reference input) 接到一個 error amplifier 內，再透過補償器 (compensator) 接回 PWM 產生器，最後完成訊號的修正。

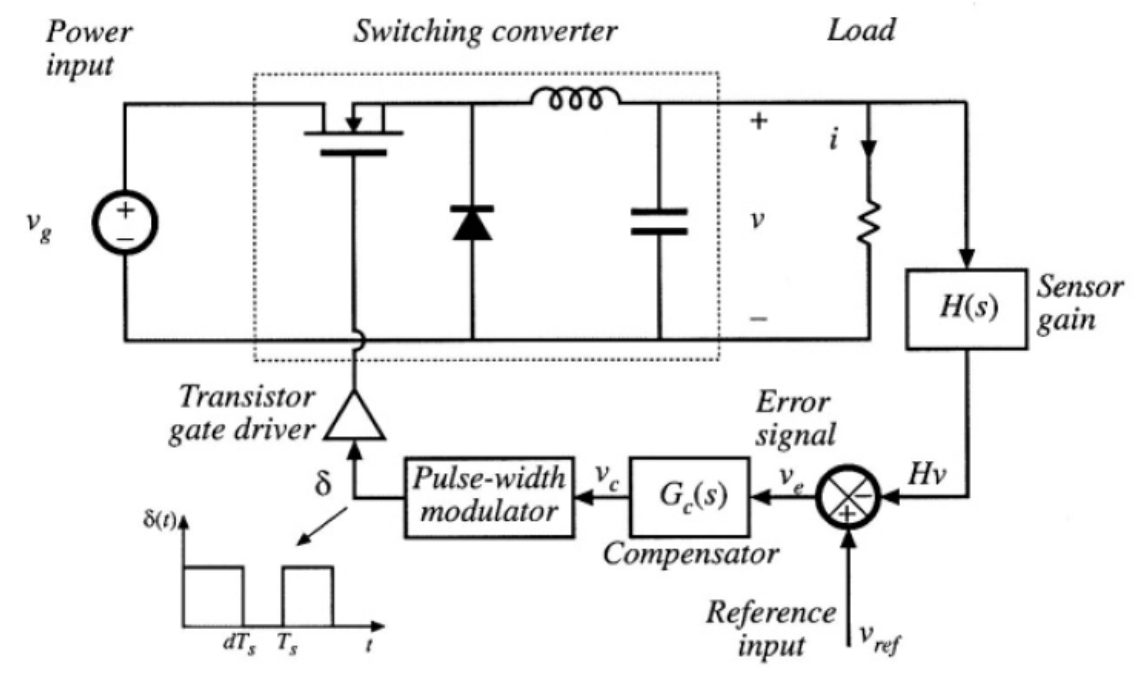圖 2-3 Closed loop buck converter design.

如果接上 PV 板組成光獵能系統，需要考慮其功率變動的問題，進行最大功率點追蹤 (Maximum power point tracking，簡稱 MPPT)。 其原理是為了因應日照變化，讓負載配合其最大功率輸出的負載曲線來做調整，進一步將系統調整到最佳的效率。 將其 MPPT 系統整合進 closed loop 的電路呈現如下圖 2-4 ¹⁶，整合 MPPT 訊號與電壓迴授訊號進入 PWM 產生器內，利用 MPPT 尋求最高功率點，再利用補償器穩壓，最後達到所需的電壓輸出。

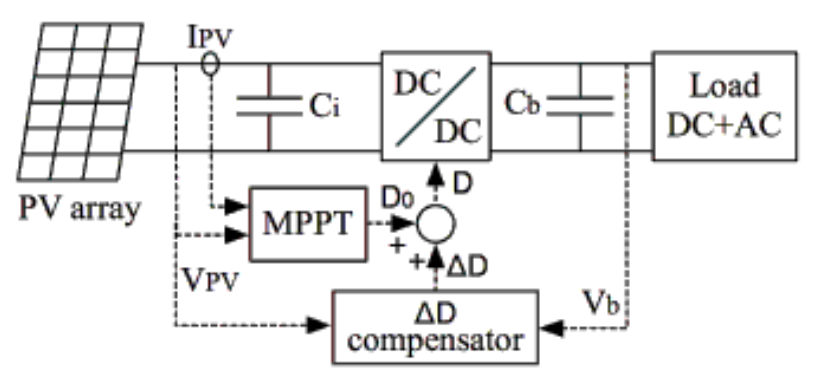圖 2-4 Closed loop buck converter with MPPT.

最常見的 MPPT 控制器策略為 Perturb and observe (P&O)，其方法是透過不斷的調整電壓並觀察其功率變化，來找出最大功率點。 雖然其尋找速度快，然而需要進行較複雜的電路運算，且因為必須不斷進行測量和觀察，使得其輸出電壓會在最大功率點附近進行震盪，再成不理想的直流輸入，需要外接濾波電容來降低其影響。 另一種常見的方式為開路電壓法，是將其電壓調整到開路電壓的固定倍率，儘管成本較低，卻因為需要時常將負載開路，造成能源的浪費，進一步使得其最大功率點降低。

三、驗證結果

本次實驗設計之電路圖如下圖 3-1，預計利用一顆 F4905L 的 P 型 MOSFET (M1)、一顆 75545P 的 N 型 MOSFET (M2)、一顆 4.7μH 電感(L1)，一顆 10μF 電容(C1)，以及一顆 15Ω 電阻(R1)。 其中，Input 為經過雙開關的電壓輸入點，Output 為電壓輸出點。

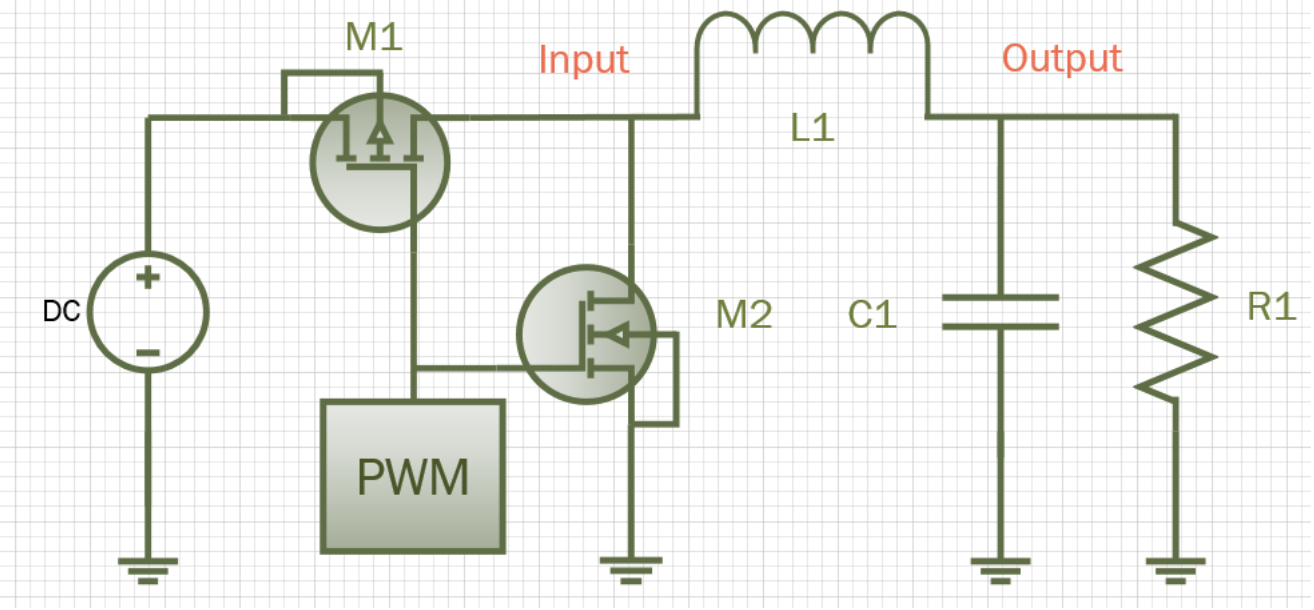圖 3-1 Buck converter 電路圖

設計 Duty Cycle 為 1.8/5，MOSFET 之 L = 0.35μ、W = 20μ、M = 1k，之後利用 HSPICE 模擬 buck converter 的電路後，預估波型如下圖 3-2 所示。

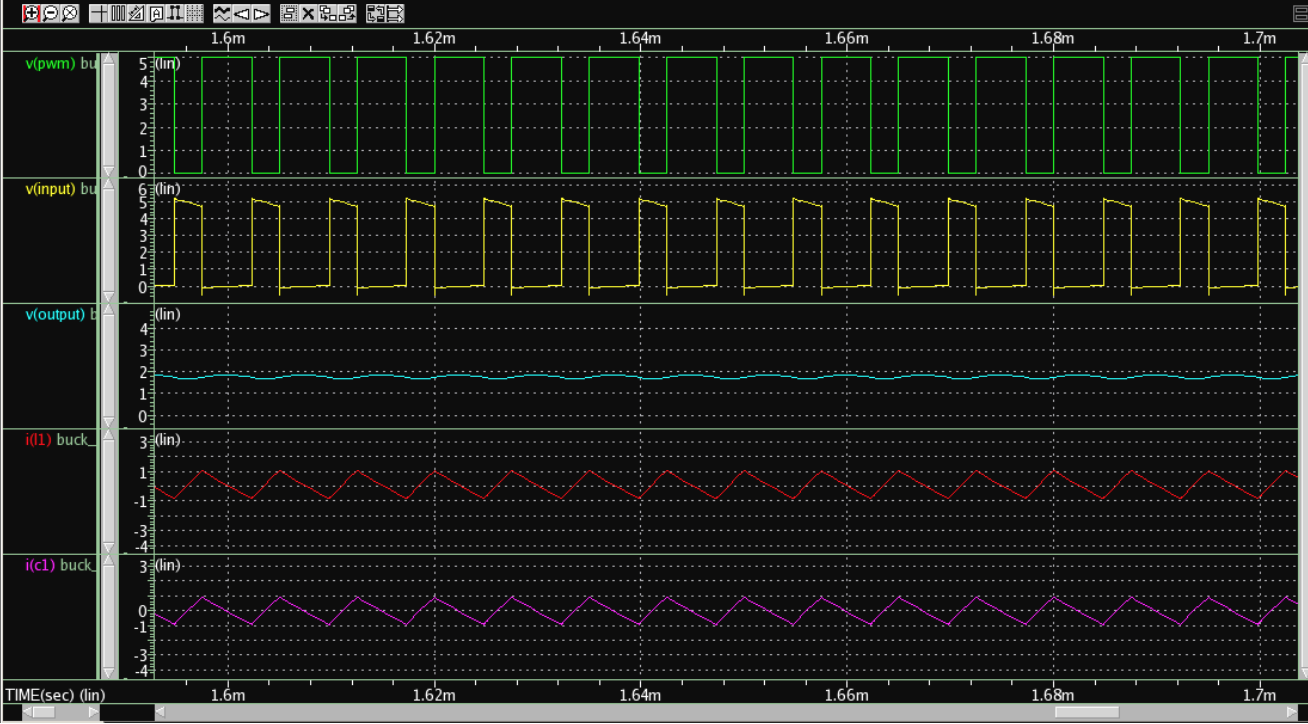圖 3-2 HSPICE 電路模擬圖

由上圖可見，輸出平均值為 1.775V，其中大部分的電流 ripple 皆被電容所濾除，只留下穩定的直流電壓，誤差值為 1.39%。

如果帶入公式 $V_{ripple} = \dfrac{D(1-D)}{8LC}\:V_S\:T^2$，計算得電壓 ripple ≅ 0.086V，實際測量值約 0.085V，誤差 1.36%。

如果討論電感電流，帶入前文公式：

$I_{Max} = DV_S\:(\dfrac{1}{R}+\dfrac{1-D}{2L}\:T)$

$I_{min} = DV_S\:(\dfrac{1}{R}-\dfrac{1-D}{2L}\:T)$

電感電流的理論最大值 $I_{L,Max} \approx 1.039$，實際測量值約 1.05，誤差 1.04%。
電感電流的理論最小值 $I_{L,min} \approx -0.799$，實際測量值約 -0.814，誤差 1.08%。

整體而言，電路誤差值皆在 2% 以內，其誤差來源主要是 MOSFET 的電壓 消耗不穩定所導致。 實際焊接成品如下圖 3-3 所示，外接正負極電源和一根 PWM 訊號線。

圖 3-3 Buck converter 硬體電路實現

四、結論

本次專題從 Open-loop buck converter 的基礎電路進行分析，進一步探討其元件設計的相關特性，之後再討論到 Closed-loop 的電路設計，以及 MPPT 的簡易應用與比較，最後進行 HSPICE 的測量，並實作出成果。

光獵能系統的應用範圍相當廣泛，其直流轉換器的設計也相當重要。 這次專題從理論到實作從頭走了一遍，儘管細節仍有不足，但對其設計原理和領域前瞻性皆有更深刻的認知。 期望後人能將光獵能系統發展得更加完備，解決其輸出震盪的問題，進一步增加使用便利性，達到成品的普及化。

五、參考文獻